Please also see the Neurostats web page
Computational Neuroscience and Analysis of Neural Data
Brain science seeks to understand the myriad functions of the brain in terms of principles that lead from molecular interactions to behavior. Although the complexity of the brain is daunting and the field seems brazenly ambitious, painstaking experimental efforts have made impressive progress. While investigations, being dependent on methods of measurement, have frequently been driven by clever use of the newest technologies, many diverse phenomena have been rendered comprehensible through interpretive analysis, which has often leaned heavily on mathematical and statistical ideas. These ideas are varied, but a central framing of the problem has been to “elucidate the representation and transmission of information in the nervous system” (Perkel and Bullock 1968). In addition, new and improved measurement and storage devices have enabled increasingly detailed recordings, as well as methods of perturbing neural circuits, with many scientists feeling at once excited and overwhelmed by opportunities of learning from the ever-larger and more complex data sets they are collecting. Thus, computational neuroscience has come to encompass not only a program of modeling neural activity and brain function at all levels of detail and abstraction, from sub-cellular biophysics to human behavior, but also advanced methods for analysis of neural data.
The paragraph above comes from this paper. I am broadly interested in analysis of neural data (the basics of which are covered in my book on this subject), but most of my publications have concerned statistical analysis of spike train data (which could get merged with analysis of local field potentials, as together spike trains and local field potentials represesnt neural activity recorded from electrodes). The following paper gives a quick overview (in pictorial form, at the top) of our work in this area, while also summarizing relevant literature: Kass, R.E., Bong, H., Olarinre, T., Xin, Q., and Urban, K. (2023) Identification of interacting neural populations: Methods and statistical considerations, Journal of Neurophysiology, 130:475-496.
There is also a web page containing an overview of research published by me and my colleagues: Contributions to Analysis of Neural Spike Train and Local Field Potential Data.
Related Software (OLD):
Publications (other than books)
Selected Papers (see CV for complete list or my Google Scholar page).
- Categorized papers on spike train analysis, with overview
- Selected papers: 2011-2024
- Selected papers: 2001-2010
- Selected papers: Pre-2001
About My Publications
I would classify my publications as (1) conceptual articles and commentaries, (2) spelling out details in theory and methods, (3) supposedly substantial new theory and methods, (4) applications, and (5) books; the topics are (a) differential geometry in statistical inference, (b) Bayesian inference, (c) statistics in neuroscience, generally (d) neural decoding and brain-machine interface, (e) analysis of neural activity from single and multiple electrodes, and (f) statistics education.
This two-way scheme does not form a set of disjoint classes. For instance, everyone would, I think, say that a typical article has both conceptual and methodological aspects; and there are, of course, overlaps in the topics, too. The reason I'm spelling this out is that I believe I am a little unusual (in the world of statistical research) because I have been heavily invested in category (1), especially review articles, for reasons articluated here. Also, the explanation for my somewhat quirky attraction to category (2), even when the details may seem minor, is captured by this quote (which I'm paraphrasing) from the great David Blackwell, "I never wanted to do research, I just wanted to understand. And sometimes, in order to understand, you have to do research." Good examples of what I'm calling "details," which also illuminate concepts, are a 1990 paper on data-translated likelihood, a 2006 paper with Valerie Ventura on spike count correlation and trial-to-trial variability, a 2008 paper with Shinsuke Koyama on the relationship between GLM point process models and LIF models, and a 2019 paper on the form in which history effects enter GLM point process models and its effect on model "stability."
The big questions I've had, and still have, are these: What is the relationship between precise mathematical statements and their conceptual counterparts (i.e, the verbal descriptions of theories or methods, their motivations, their accomplishments)? Given the messiness of data-analytic reality, how should we think about the value of statistical theory? When and how is it useful for statistical models to be statements about the empirical world (e.g., in neuroscience)? What are effective ways to communicate statistical ideas?
2011-2024
Behseta, S. and Kass, R.E. (2024) A conversation with Stephen M. Stigler, Statistical Science, 39: 192-208.
Bong, H., Ventura, V., Yttri, E.A., Smith, M.A. and Kass, R.E. (2023) Cross-population amplitude coupling in high-dimensional oscillatory neural time series, submitted, pre-publication draft here.
Glasgow, N.G., Chen, Y., Korngreen, A., Kass, R.E., and Urban, N.N. (2023) A biophysical and statistical modeling paradigm for connecting neural physiology and function. Journal of Computational Neuroscience, 51: 263-282.
Kass, R.E., Bong, H., Olarinre, T., Xin, Q., and Urban, K. (2023) Identification of interacting neural populations: Methods and statistical considerations, Journal of Neurophysiology, 130:475-496.
Urban, K., Bong, H., Orellana, J., and Kass, R.E. (2023) Oscillating neural circuits: Phase, amplitude, and the complex normal distribution, Canadian Journal of Statistics, 51: 824-851.
Chen, Y.. Douglas, H., Medina. B.J., Olarinre, M., Siegle, J.H., and Kass, R.E. (2022) Population burst propagation across interacting areas of the brain, Journal of Neurophysiology, 128: 1578-1592.
Klein, N., Siegle, J.H., Teichert, T. and Kass, R.E. (2021). Cross-population coupling of neural activity based on Gaussian process current source densities. PLoS Computational Biology, 17: e1009601.
Behseta, S. and Kass, R.E. (2021) A conversation with Emery Brown, Chance, 34.
Bong, H., Liu, Z., Ren, Z., Smith, M.A., Ventura, V. and Kass, R.E. (2021) Latent Dynamic Factor Analysis of High-Dimensional Neural Recordings, 34th Conference on Neural Information Processing Systems (NeurlPS), Vancouver, Canada, to appear. 3 minute video summary here.
Grisham, W., Abrams, M., Babiec, W.E., Fairhall, A.L., Kass, R.E., Wallisch, P. and Olivo, R. (2021) Teaching Computation in Neuroscience: Notes on the 2019 Society for Neuroscience Professional Development Workshop on Teaching, The Journal of Undergraduate Neuroscience Education (June), 19: A185--A191.
Kass, R. E. (2021) The Two Cultures: Statistics and Machine Learning in Science, Observational Studies, 7: 135--144.
Klein, N., Orellana, J., Brincat, S., Miller, E.K., and Kass, R.E. (2020) Torus graphs for multivariate phase coupling analysis, Annals of Applied Statistics, 14: 635-660, and supplementary material. Tutorial and code here.
Kass, R.E. and Matheo, L.M. (2019) Letter to the Editor concerning "Brain change in addiction as learning, not disease," The New England Journal of Medicine, 380: 301.
Yang, Y., Tarr, M.J., Kass, R.E., and Aminoff, E.M. (2019) Exploring spatio-temporal neural dynamics of the human visual cortex, Human Brain Mapping, 40: 4213-4238.
Chen, Y., Xin, Q., Ventura, V., and Kass, R.E. (2019) Stability of point process spiking neuron models, Journal of Computational Neuroscience, 46: 19-32.
Kass, R.E., Amari, S.-I., Arai, K., Brown, E.N., Diekman, C.O., Diesmann, M., Doiron, B., Eden, U.T., Fairhall, A.L., Fiddyment, G.M., Fukai, T., Grün, S., Harrison, M.T., Helias, M., Nakahara, H., Teramae, J.-N., Thomas, P.J., Reimers, M., Rodu, J., Rotstein, H.G., Shea-Brown, E., Shimazaki, H., Shinomoto, S., Yu, B.M., and Kramer, M.A. (2018) Computational neuroscience: Mathematical and statistical perspectives , Annual Review of Statistics and its Application, 5: 183-214. Pre-publication draft available here.
Rodu, J., Klein, N., Brincat, S.L., Miller, E.K., and Kass, R.E. (2018) Detecting multivariate cross-correlation between brain regions , Journal of Neurophysiology, 120: 1962-1972.
Vinci, G., Ventura, V., Smith, M.A., and Kass, R.E. (2018) Adjusted regularization of cortical covariance , Journal of Computational Neuroscience, 45: 83-101.
Vinci, G., Ventura, V., Smith, M.A., and Kass, R.E. (2018) Adjusted regularization in latent graphical models: Application to multiple-neuron spike count data , Annals of Applied Statistics, 12: 1068-1095. Pre-publication draft and supplementary material.
Zhou, P., Resendez, S.L., Rodriguez-Romaguera, J., Stuber, G.D., Jimenez, J.C., Hen, R., Keirbek, M.A., Neufeld, S.Q., Sabatini, B.L., Kass, R.E., and Paninski, L. (2018) Efficient and accurate extraction of in vivo calcium signals from microendoscopic video data, eLife, 7: e28728 DOI: 10.7554/elife.28728.
Arai, K. and Kass, R.E. (2017) Inferring oscillatory modulation in neural spike trains , PLoS Computational Biology, 13: e1005596.
Koerner, F. S., Anderson, J. R., Fincham, J. M., and Kass, R. E. (2017) Change-point detection of cognitive states across multiple trials in functional neuroimaging, Statistics in Medicine, 36: 618-642.
Orellana, J., Rodu, J., and Kass, R.E. (2017) Population vectors can provide near optimal integration of information, Neural Computation, 29: 2021-2029.
Suway, S.B., Orellana, J. McMorland, A.J.C., Fraser, G.W., Liu, Z., Velliste, M., Chase, S.M., Kass, R.E., and Schwartz, A.B. (2017) Temporally segmented directionality in the motor cortex, Cerebral Cortex, 7: 1-14.
Wood, J., Simon, N.W., Koerner, F.S., Kass, R.E., and Moghaddam, B. (2017) Networks of VTA neurons encode real-time information about uncertain numbers of actions executed to earn a reward, Frontiers in Behavioral Neuroscience, 11: 140.
Yang, Y., Xu, Y., Jew, C.A., Pyles, J.A., Kass, R.E., and Tarr, M.J. (2017) Exploring the spatio-temporal neural basis of face learning, Journal of Vision, 17: 1.doi:10.1167/17.6.1.
Zhang, Q., Borst, J.P., Kass, R.E., and Anderson, J.A. (2017) Inter-subject alignment of MEG datasets in a common representational space, Human Brain Mapping, 38: 4287-4301.
Yang, Y., Aminoff, E., Tarr, M. and Kass, R.E. (2016) A state-space model of cross-region dynamic connectivity in MEG/EEG, Advances in Neural Information Processing Systems (NIPS), 29: 1226--1234.
Hefny, A., Kass, R.E., Khanna, S., Smith, M., and Gordon, G.J. (2016) Fast and improved SLEX analysis of high-dimensional time series , in Machine Learning and Interpretation in Neuroimaging: Beyond the Scanner, Lecture Notes on Artificial Intelligence, edited by G. Cecchi, K.K. Chang, G. Langs, B. Murphy, I. Rish, and L. Wehbe, Springer, Volume 9444, pp 94--103.
Kass, R.E., Caffo, B., Davidian, M., Meng, X.-L., Yu, B., and Reid, N. (2016) Ten simple rules for effective statistical practice, PLoS Computational Biology, 12:e1004961. 5 minute video version
Vinci, G., Ventura, V., Smith, M.A., and Kass, R.E. (2016) Separating spike count correlation from firing rate correlation , Neural Computation, 28: 849--881.
Yang, Y., Tarr, M.J., and Kass, R.E. (2016) Estimating learning effects: a short-time Fourier transform regression model for MEG source localization , in Machine Learning and Interpretation in Neuroimaging: Beyond the Scanner, Lecture Notes on Artificial Intelligence, edited by G. Cecchi, K.K. Chang, G. Langs, B. Murphy, I. Rish, and L. Wehbe, Springer, Volume 9444, pp 69--82.
Castellanos, L., Vu, V.Q., Perel, S., Schwartz, A., and Kass, R.E. (2015) A multivariate Gaussian process factor analysis model for hand shape during reach-to-grasp movements , Statistica Sinica, 25: 5--24. supplementary material
Kass, R.E. (2015) The gap between statistics education and statistical practice. (Comment on "Mere renovaton is too little too late: we need to re-think our undergraduate curriculum from the ground up" by George Cobb), The American Statistician, 69, Online Discussion: Special Issue on Statistics and the Undergraduate Curriculum.
Scott, J.G., Kelly, R.C., Smith, M.A., Zhou, P. and Kass, R.E. (2015) False discovery rate regression: an application to neural synchrony detection in primary visual cortex , Journal of the American Statistical Association, 110: 459--471.
Wang, W., Tripathy, S.J., Padmanabhan, K., Urban, N.N., and Kass, R.E. (2015) An empirical model for reliable spiking activity , Neural Computation, August 2015, 27: 8, 1609--1623.
Zhou, P., Burton, S.D., Snyder, A.C., Smith, M.A., Urban, N.N. and Kass, R.E. (2015) Establishing a statistical link between network oscillations and neural synchrony, PLoS Computational Biology, 11: e1004549. doi: 10.1371/journal.pcbi.1004549
Kass, R.E. (2014) Spike train , in Encyclopedia of Computational Neuroscience, edited by D. Jaeger and R. Jung. Springer.
Kass, R.E. and many others (2014) Statistical Research and Training Under the BRAIN Initiative , report of a working group of the American Statistical Association.
Harrison, M.T., Amarasingham, A., and Kass, R.E. (2013) Statistical identification of synchronous spiking, in Spike Timing: Mechanisms and Function, edited by P. Di Lorenzo and J. Victor. Taylor and Francis, pp. 77--120.
Koyama, S., Omi, T., Kass, R.E. and Shinomoto, S. (2013) Information transmission using non-Poisson regular firing, Neural Computation, 25: 854--876.
Perez, O., Kass, R.E., and Merchant, H. (2013) Trial time warping to discriminate stimulus-related from movement-related neural activity, Journal of Neuroscience Methods, 212: 203-210.
Kelly, R.C. and Kass, R.E. (2012) A framework for evaluating pairwise and multiway synchrony among stimulus-driven neurons, Neural Computation, 24: 2007--2032. (Note: title of first draft was "Detecting multi-way synchrony in the presence of two-way synchrony among stimulus-driven neurons.")
Zhang, Y., Schwartz, A.B., Chase, S.M., and Kass, R.E. (2012) Bayesian learning in assisted brain-computer interface tasks, Engineering in Medicine and Biology, 2012 Annual International Conference of the IEEE (EMBC), 2740--2743.
Xu, Y., Sudre, G.P., Wang, W., Weber, D.J., and Kass, R.E. (2011) Characterizing global statistical significance of spatio-temporal hot spots in MEG/EEG source space via excursion algorithms, Statistics in Medicine, 30: 2854--2866.
Kass, R.E. (2011) Statistical inference: the big picture, with discussion by Andrew Gelman, discussion by Steven Goodman, discussion by Rob McCulloch, discussion by Hal Stern, and rejoinder , Statistical Science, 26: 1--20.
Kass, R.E., Kelly, R.C., and Loh, W.-L. (2011) Assessment of synchrony in multiple neural spike trains using loglinear point process models, Annals of Applied Statistics, 5: 1262--1292.
2001-2010
Chase, S.M., Schwartz, A.B., and Kass, R.E. (2010) Latent inputs improve estimates of neural encoding in motor cortex, Journal of Neuroscience, 30: 13873--13882.
Kass, R.E. (2010) Comment: How should indirect evidence be used? Statistical Science, 25: 166-169.
Kelly, R.C, Smith, M.A., Kass, R.E., and Lee, T.-S. (2010) Accounting for network effects in neuronal responses using L1 penalized point process models, Advances in Neural Information Processing Systems (NIPS), 23.
Kelly, R.C., Smith, M.A., Kass, R.E., and Lee, T.-S. (2010) Local field potentials indicate network state and account for neuronal response variability, Journal of Computational Neuroscience, 29: 567--579.
Koyama, S., Castellanos Perez-Bolde, L., Shalizi, C.R., and Kass, R.E. (2010) Approximate methods for state-space models, Journal of the American Statistical Association, 105: 170-180. DOI: 10.1198/jasa.2009.tm08326.
Koyama, S., Chase, S.M., Whitford, A.S., Velliste, M., Schwartz, A.B., and Kass, R.E.(2010) Comparison of brain-computer interface decoding algorithms in open-loop and closed-loop control, Journal Computational Neuroscience, 29: 73--87.
Paninski, L., Brown, E.N., Iyengar, S., and Kass, R.E. (2010) Statistical models of spike trains, in Stochastic Methods in Neuroscience , edited by C. Liang and G.J. Lord, Oxford, pp. 272-296.
Tokdar, S., Xi, P., Kelly, R.C., and Kass, R.E. (2010) Detection of bursts in extracelluar spike trains using hidden semi-Markov point process models, Journal of Computational Neuroscience, 29: 203--212.
Wang, W., Sudre, G.P., Xu, Y., Kass, R.E., Collinger, J.L., Degenhart, A.D., Bagic, A.I., and Weber, D.J. (2010) Decoding and cortical source localization for intended movement direction with MEG, Journal of Neurophysiology, 104: 2451--2461.
Behseta, S., Berdyyeva, T., Olson, C.R., and Kass, R.E. (2009) Bayesian correction for attenuation of correlation in multi-trial spike count data, Journal of Neurophysiology, 101:2186-2193.
Brown, E.N. and Kass, R.E. (2009) What is Statistics? (with discussion), American Statistician, 63:105-123.
Chase, S.M., Schwartz, A.B., and Kass, R.E. (2009) Bias, optimal linear estimation, and the differences between open-loop simulation and closed-loop performance of spiking-based brain computer interface algorithms, Neural Networks, 22:1203-1213.
Kass, R.E. (2009) The importance of Jeffreys's Legacy (Comment on Robert, Chopin, and Rousseau) Statistical Science, 24: 2, 179-182.
Vu, V.Q., Yu, B. and Kass, R.E. (2009) Information in the non-stationary case, Neural Computation, 21:688-703.
Jarosiewicz, B., Chase, S.M., Fraser, G.W., Velliste, M. Kass, R.E., and Schwartz, A.B.(2008) Functional network reorganization during learning in a brain-machine interface paradigm, Proceedings of the National Academy of Sciences,105:19486-19491.
Koyama, S. and Kass, R.E. (2008) Spike train probability models for stimulus-driven leaky integrate-and-fire neurons, Neural Computation, 20:1776-1795.
Wallstrom, G., Liebner, J., and Kass, R.E. (2008) An implementation of Bayesian Adaptive Regression Splines (BARS) in C with S and R wrappers, Journal of Statistical Software, 26: 1-25. (online at http://www.jstatsoft.org).
Behseta, S., Kass, R.E., Moorman, D. and Olson, C. (2007) Testing Equality of Several Functions: Analysis of Single-Unit Firing Rate Curves Across Multiple Experimental Conditions, Statistics in Medicine, 26: 3958-3975.
Brockwell, A.E., Kass, R.E., and Schwartz, A.B. (2007) Statistical signal processing and the motor cortex, Proceedings of the IEEE, 95: 881-898.
Vu, V.Q., Yu, B., and Kass, R.E. (2007) Coverage Adjusted Entropy Estimation Statistics in Medicine, 26: 4039-4060.
Kass, R.E. (2006) Kinds of Bayesians (Comment on articles by Berger and by Goldstein), Bayesian Analysis, 1: 437-440.
Kass, R.E. and Ventura, V. (2006) Spike count correlation increases with length of time interval in the presence of trial-to-trial variation, Neural Computation, 18:2583-2591.
Behseta, S., Kass, R.E., and Wallstrom, G.L. (2005) Hierarchical models for assessing variability among functions, Biometrika, 92: 419-434.
Behseta, S. and Kass, R.E. (2005) Testing Equality of Two Functions using BARS, Statistics in Medicine, 24:3523-34.
Kass, R.E., Ventura, V., and Brown, E.N. (2005) Statistical issues in the analysis of neuronal data, Journal of Neurophysiology, 94: 8-25.
Kaufman, C.G., Ventura, V., and Kass, R.E. (2005) Spline-based nonparametric regression for periodic functions and its application to directional tuning of neurons, Statistics in Medicine, 24: 2255-2265.
Ventura, V., Cai, C., and Kass, R.E. (2005) Statistical assessment of time-varying dependence between two neurons, Journal of Neurophysiology, 94: 2940-2947.
Ventura, V. Cai, C., and Kass, R.E. (2005) Trial-to-trial variability and its effect on time-varying dependence between two neurons, Journal of Neurophysiology, 94: 2928-2939.
Brockwell, A.E., Rojas, A.L., and Kass, R.E. (2004) Recursive Bayesian decoding of motor cortical signals by particle filtering, Journal of Neurophysiology, 91: 1899--1907.
Brown, E.N., Kass, R.E., and Mitra, P.N. (2004) Multiple neural spike trains analysis: state-of-the-art and future challenges. Nature Neuroscience, 7: 456--461.
Wallstrom, G.A., Kass, R.E., Miller, A., Cohn, J.F., and Fox, N.A.(2004) Automatic correction of ocular artifacts in the EEG: A comparison of regression-based and component-based methods, International Journal of Psychophysiology, 53: 105--119.
Kass, R.E., Ventura, V. and Cai, C. (2003) Statistical smoothing of neuronal data, Network: Computation in Neural Systems, 14: 5--15.
Brown, B.N., Barbieri, R, Ventura V., Kass R.E., and Frank L.M. (2002) The time-rescaling theorem and its applications to neural spike train data analysis, Neural Computation, 14: 325--346.
Ventura V., Carta R., Kass R.E., Gettner, S.N., and Olson, C.R., (2002) Statistical analysis of temporal evolution in single-neuron firing rates, Biostatistics, 1: 1--20.
Wallstrom, G.L, Kass, R.E., Miller, A., Cohn, J.F., and Fox, N.A. (2002) Correction of ocular artifacts in the EEG using Bayesian adaptive regression splines, in Case Studies in Bayesian Statistics, Vol VI, eds. Gatsonis, C., Carriquiry, A., Higdon, D., Kass, R.E., Pauler, D., and Verdinelli, I., pp. 351-366, Springer-Verlag.
Daniels, M.J. and Kass, R.E. (2001) Shrinkage estimators for covariance matrices, Biometrics, 57, 1173-1184.
DiMatteo, I., Genovese, C.R., and Kass, R.E. (2001) Bayesian curve-fitting with free-knot splines, Biometrika, 88: 1055-1071.
Kass, R.E., and Ventura, V. (2001) A spike-train probability model, Neural Computation, 13: 1713-1720.
Pre-2001
Olson, C.R., Gettner, S.N., Ventura, V., Carta, R., and Kass, R.E. (2000) Neuronal activity in Macaque supplementary eye field during planning of saccades in response to pattern and spatial cues, Journal of Neurophysiology, 84: 1369-1384.
Daniels, M.J. and Kass, R.E. (1999) Nonconjugate Bayesian estimation of covariance matrices and its use in hierarchical models, Journal of the American Statistical Association, 94, 1254-1263.
Daniels, M.J. and Kass, R.E. (1998) A note on first-stage approximation in two-stage hierarchical models, Sankhya: The Indian Journal of Statistics, 60, B: 19-30.
Kass, R.E. (1998) Comment on R.A. Fisher in the 21st Century, by Bradley Efron, Statistical Science, 13: 95-122
Kass, R.E., Carlin, B.P., Gelman, A., and Neal, R. (1998) MCMC in practice: a roundtable discussion, American Statistician, 52: 93-100.
Gitelman, A.I., Risbey, J.S., Kass, R.E. and Rosen, R.D. (1997) Trends in the surface meridional temperature gradient Geophysical Research Letters, Vol. 24, (10). 1243-1246.
Kass, R.E. and Wasserman, L.A. (1996) The selection of prior distributions by formal rules, Journal of the American Statistical Association, 91: 1343-1370.
Kass, R.E. and Wasserman, L.A. (1995) A reference Bayesian test for nested hypotheses and its relationship to the Schwarz criterion, Journal of the American Statistical Association, 90: 928-934.
Kass, R.E. and Raftery, A. (1995) Bayes Factors, Journal of the American Statistical Association, 90: 773-795.
Kass, R.E. and Slate, E.H. (1994) Some diagnostics of maximum likelihood and posterior nonnormality, The Annals of Statistics, 22: 668-695.
Kass, R.E. (1991) More about "Theory of Probability" by H. Jeffreys, Chance, 4: no. 2, p. 13.
Kass, R.E. (1990) Data-translated likelihood and Jeffreys's rules, Biometrika, 77: 107-114.
Kass, R.E., Tierney, L. and Kadane, J.B. (1990) The validity of posterior expansions based on Laplace's method, Essays in Honor of George Bernard, eds. S. Geisser, J.S. Hodges, S.J. Press, and A. Zellner, Amsterdam: North Holland, 473-488.
Kass, R.E. and Steffey, D. (1989) Approximate Bayesian inference in conditionally independent hierarchical models (parametric empirical Bayes modes), Journal of the American Statistical Association, 84: 717-726.
Tierney, L., Kass, R.E. and Kadane, J.B. (1989) Fully exponential Laplace approximations to posterior expectations and variances, Journal of the American Statistical Association, 84: 710-716.
Kass, R.E. (1989) The geometry of asymptotic inference (with discussion) Statistical Science, 4: 188-234.
Buja, A. and Kass, R.E. (1985) Comment: Some observations on ACE methodology, Journal of the American Statistical Association, 80: 602-607.
Kass, R.E. (1983) Bayes Methods for Combining the Results of Cancer Studies in Humans and Other Species: Comment, Journal of the American Statistical Association, 78: 312-313.
Book: Analysis of Neural Data

by Robert E. Kass, Uri T. Eden, and Emery N. Brown
- First Two Pages
- Testimonials
- Publisher's webpages
- Errors and Corrections
- Data
- Matlab and R code for original figures
First Two Pages
The brain sciences seek to discover mechanisms by which neural activity is generated, thoughts are created, and behavior is produced. What makes us see, hear, feel, and understand the world around us? How can we learn intricate movements, which require continual corrections for minor variations in path? What is the basis of memory, and how do we allocate attention to particular tasks? Answering such questions is the grand ambition of this broad enterprise and, while the workings of the nervous system are immensely complicated, several lines of now-classical research have made enormous progress: essential features of the nature of the action potential, of synaptic transmission, of sensory processing, of the biochemical basis of memory, and of motor control have been discovered. These advances have formed conceptual underpinnings for modern neuroscience, and have had a substantial impact on clinical practice. The method that produced this knowledge, the scientific method, involves both observation and experiment, but always a careful consideration of the data. Sometimes results from an investigation have been largely qualitative, as in Brenda Milner’s documentation of implicit memory retention, together with explicit memory loss, as a result of hippocampal lesioning in patient H.M. In other cases quantitative analysis has been essential, as in Alan Hodgkin and Andrew Huxley’s modeling of ion channels to describe the production of action potentials. Today’s brain research builds on earlier results using a wide variety of modern techniques, including molecular methods, patch clamp recording, two-photon imaging, single and multiple electrode studies producing spike trains and/or local field potentials (LFPs), optical imaging, electroencephalography (producing EEGs), and functional imaging—positron emission tomography (PET), functional magnetic resonance imaging (fMRI), magnetoencephalography (MEG)—as well as psychophysical and behavioral studies. All of these rely, in varying ways, on vast improvements in data storage, manipulation, and display technologies, as well as corresponding advances in analytical techniques. As a result, data sets from current investigations are often much larger, and more complicated, than those of earlier days. For a contemporary student of neuroscience, a working knowledge of basic methods of data analysis is indispensable.The variety of experimental paradigms across widely ranging investigative levels in the brain sciences may seem intimidating. It would take a multi-volume encyclopedia to document the details of the myriad analytical methods out there. Yet, for all the diversity of measurement and purpose, there are commonalities that make analysis of neural data a single, circumscribed and integrated subject. A relatively small number of principles, together with a handful of ubiquitous techniques—some quite old, some much newer—lay a solid foundation. One of our chief aims in writing this book has been to provide a coherent framework to serve as a starting point in understanding all types of neural data.
In addition to providing a unified treatment of analytical methods that are crucial to progress in the brain sciences, we have a secondary goal. Over many years of collaboration with neuroscientists we have observed in them a desire to learn all that the data have to offer. Data collection is demanding, and time-consuming, so it is natural to want to use the most efficient and effective methods of data analysis. But we have also observed something else. Many neuroscientists take great pleasure in displaying their results not only because of the science involved but also because of the manner in which particular data summaries and displays are able to shed light on, and explain, neuroscientific phenomenon; in other words, they have developed a refined appreciation for the data-analytic process itself. The often-ingenious ways investigators present their data have been instructive to us, and have reinforced our own aesthetic sensibilities for this endeavor. There is deep satisfaction in comprehending a method that is at once elegant and powerful, that uses mathematics to describe the world of observation and experimentation, and that tames uncertainty by capturing it and using it to advantage. We hope to pass on to readers some of these feelings about the role of analytical techniques in illuminating and articulating fundamental concepts.
A third goal for this book comes from our exposure to numerous articles that report data analyzed largely by people who lack training in statistics. Many researchers have excellent quantitative skills and intuitions, and in most published work statistical procedures appear to be used correctly. Yet, in examining these papers we have been struck repeatedly by the absence of what we might call statistical thinking, or application of the statistical paradigm, and a resulting loss of opportunity to make full and effective use of the data. These cases typically do not involve an incorrect application of a statistical method (though that sometimes does happen). Rather, the lost opportunity is a failure to follow the general approach to the analysis of the data, which is what we mean by the label “the statistical paradigm.” Our final pedagogical goal, therefore, is to lay out the key features of this paradigm, and to illustrate its application in diverse contexts, so that readers may absorb its main tenets.
Testimonials
"This is an outstanding book, that fills a real need. Assuming no background in statistics, it covers the data analysis methods neuroscientists need to
know, from standard material like hypothesis tests, to specialized methods that have recently found use in our field. It has the detail and insight needed
for those developing their own statistical methods. And for the working neurobiologist it has plenty of practical tricks, tips, and examples, coming straight
from the experts. This book is a must for anyone serious about quantitative analysis in neuroscience.”
“This book is a unique and valuable resource for any scientist who wants to approach neural data analysis in a rigorous fashion, or to gain a
broad overview of modern statistical concepts and approaches. The authors combine a crisp writing style with a number of helpful strategies, including
the use of many carefully-chosen examples from the neuroscience literature, and vivid reminders of the difference between the world of mathematical objects
and the world of data. ...The book is a one-of-a-kind resource that combines practicality, rigor, and accessibility; it is a book that was sorely needed and
is an extremely valuable reference.”
and Department of Neurology, Weill Cornell Medical College
“Analysis of Neural Data is a thorough, authoritative textbook . All relevant topics are covered in depth with examples from the literature and
thoughtful comments. . A highly readable, useful and commendable textbook!”
“Analysis of Neural Data provides an invaluable guide for neuroscientists seeking to summarize and interpret their data. The authors – leading statisticians
who have developed and applied many of the methods they describe themselves are also outstanding teachers, and the treatment they provide is at once accessible,
authoritative, comprehensive, and up-to-date.
Director, Center for Mind, Brain and Computation, Stanford University
“Written by eminent statisticians, this book covers a range of topics from basic mathematics to state-of-the-art statistical analyses of neural data.
Researchers conducting experiments will learn the principles of data analysis and will begin analyzing data using the methods provided. Theoreticians
will be introduced to more than 100 intriguing experiments that will teach them to form persuasive interpretations. Analysis of Neural Data should
become a standard reference for neuroscience research.”
Publisher's webpages:
- Springer webpages for the book may be found here.
- Reviews on Springer webpage for the book may be found here
Errors and Corrections:
May be found here.Corrections to first printing: The publication process introduced so many errors that Springer agreed to do another printing right away. This gave us a chance to find some of our own errors, too. Corrections may be found here. (Many figures were also re-done, to provide color when useful; we had been unaware that color would be used in printing.)
Data:
- spike trains from a rat's hippocampus - used in Chapter 14
- local field potentials - used in Chapter 18
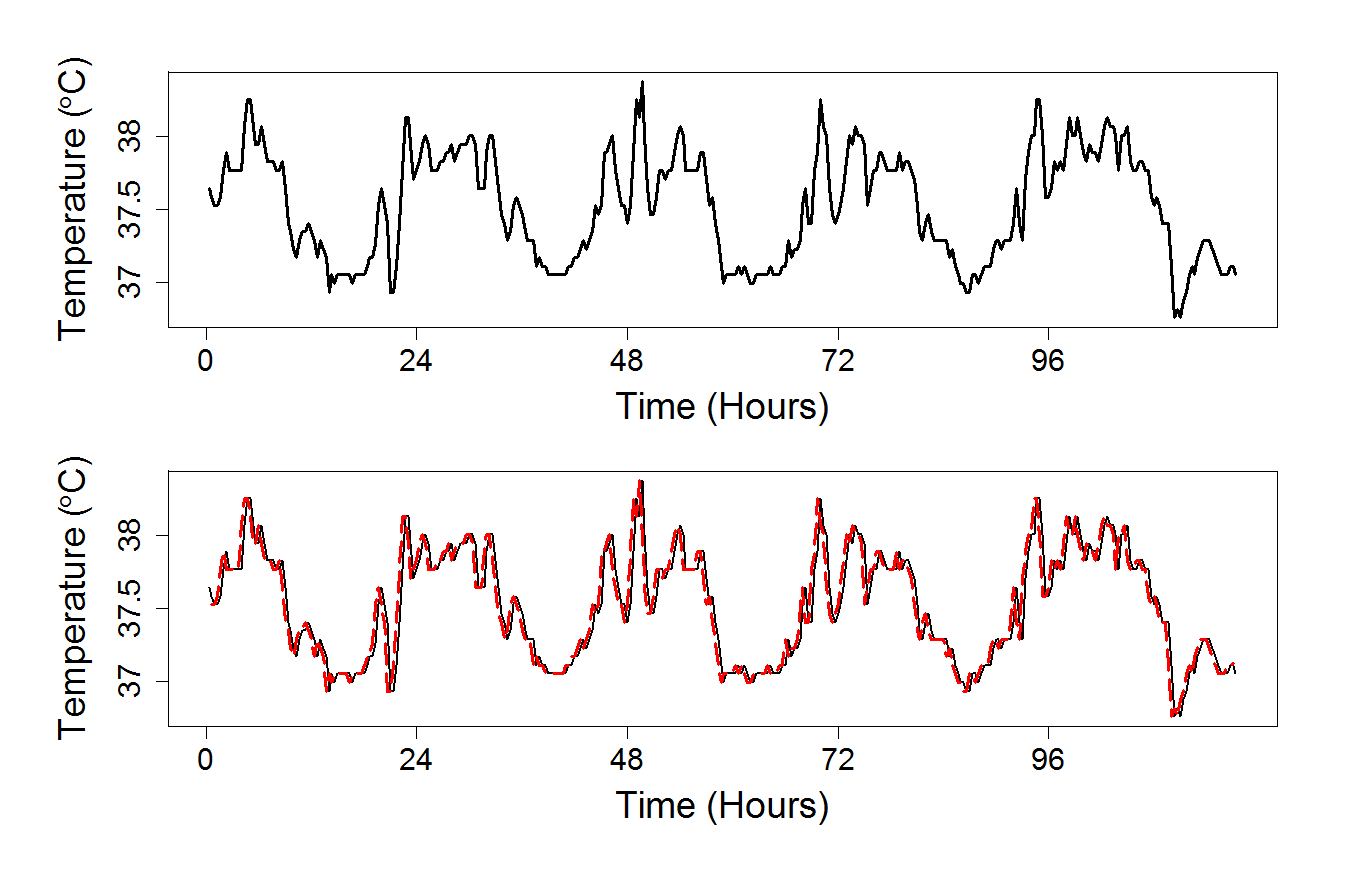
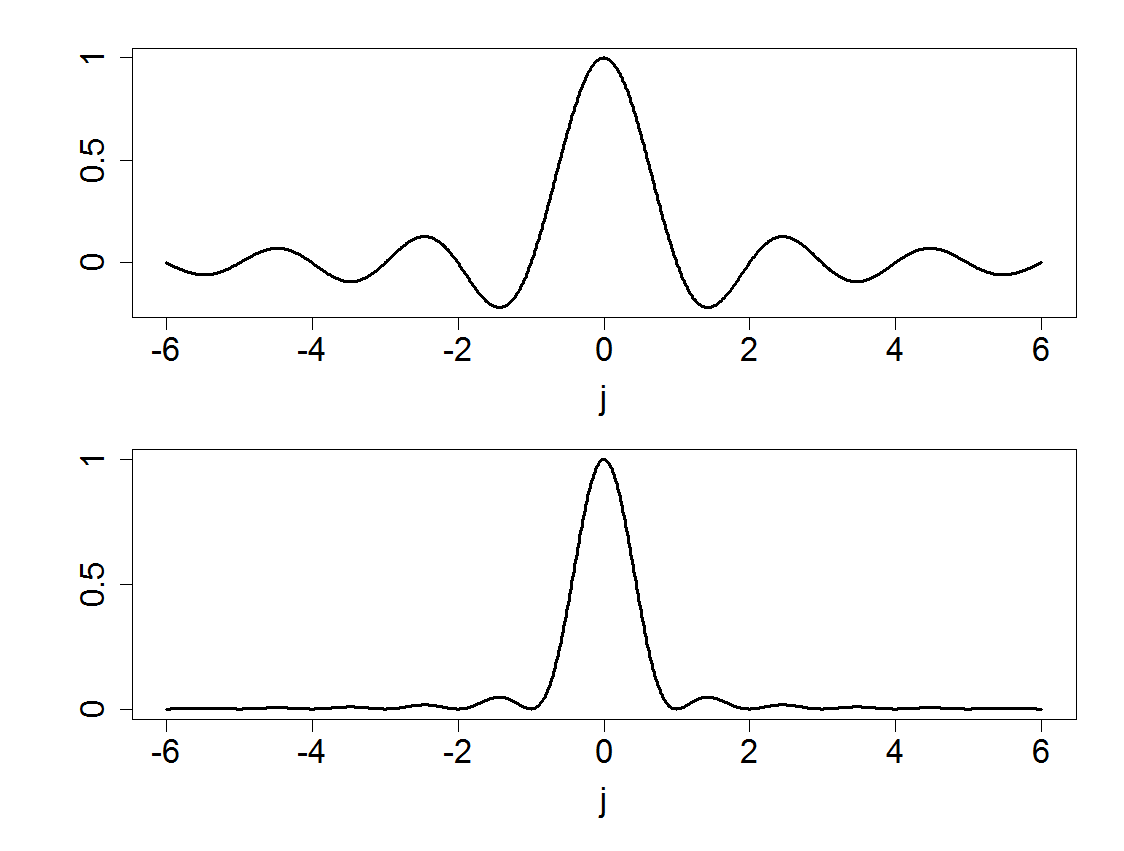
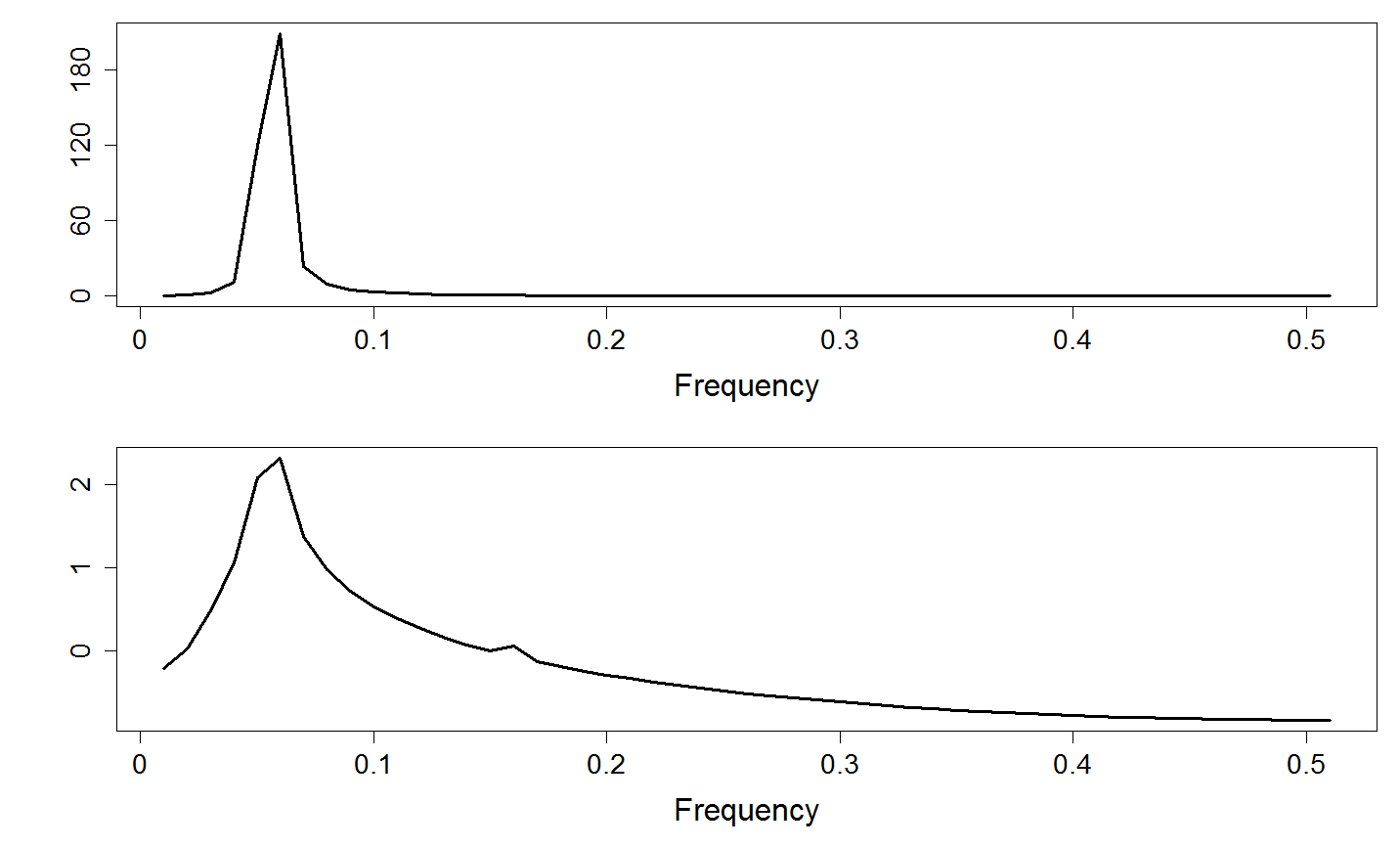
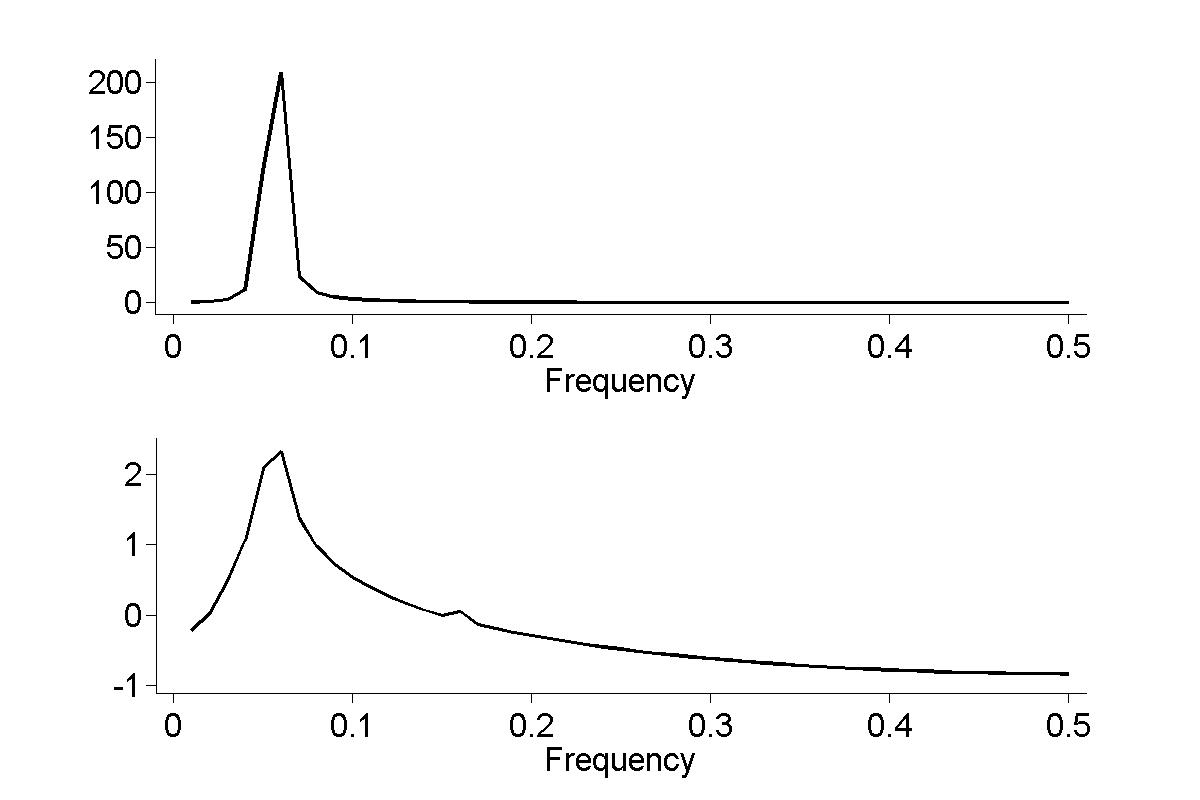
- core temperature of a human subject over 24 hours - Used in Chapter 18
- spike counts from a motor cortical neuron - used in Chapter 3
Matlab and R code for original figures in book is available below
Code (below) was contributed by Elan Cohen, Uri Eden, Rob Kass, Spencer Koerner, and Ryan Sieberg.
New versions of code were created and/or edited by Spencer Koerner and Patrick Foley. This website was created by Patrick Foley.
1 - Introduction
2 - Exploring Data
3 - Probability and Random Variables
4 - Random Vectors
5 - Important Probability Distributions
6 - Sequences of Random Variables
7 - Estimation and Uncertainty
8 - Estimation in Theory and in Practice
9 - Propagation of Uncertainty and the Bootstrap
10 - Models, Hypotheses, and Statistical Significance
11 - General Methods for Testing Hypotheses
12 - Linear Regression
13 - Analysis of Variance
14 - Generalized Linear and Nonlinear Regression
16 - Bayesian Methods
18 - Time Series
19 - Point Processes
1 - Introduction
Figure 1.4
 |
 |
|
| |
|
2 - Exploring Data
Figure 2.1
 |
 |
|
| |
|
Figure 2.2
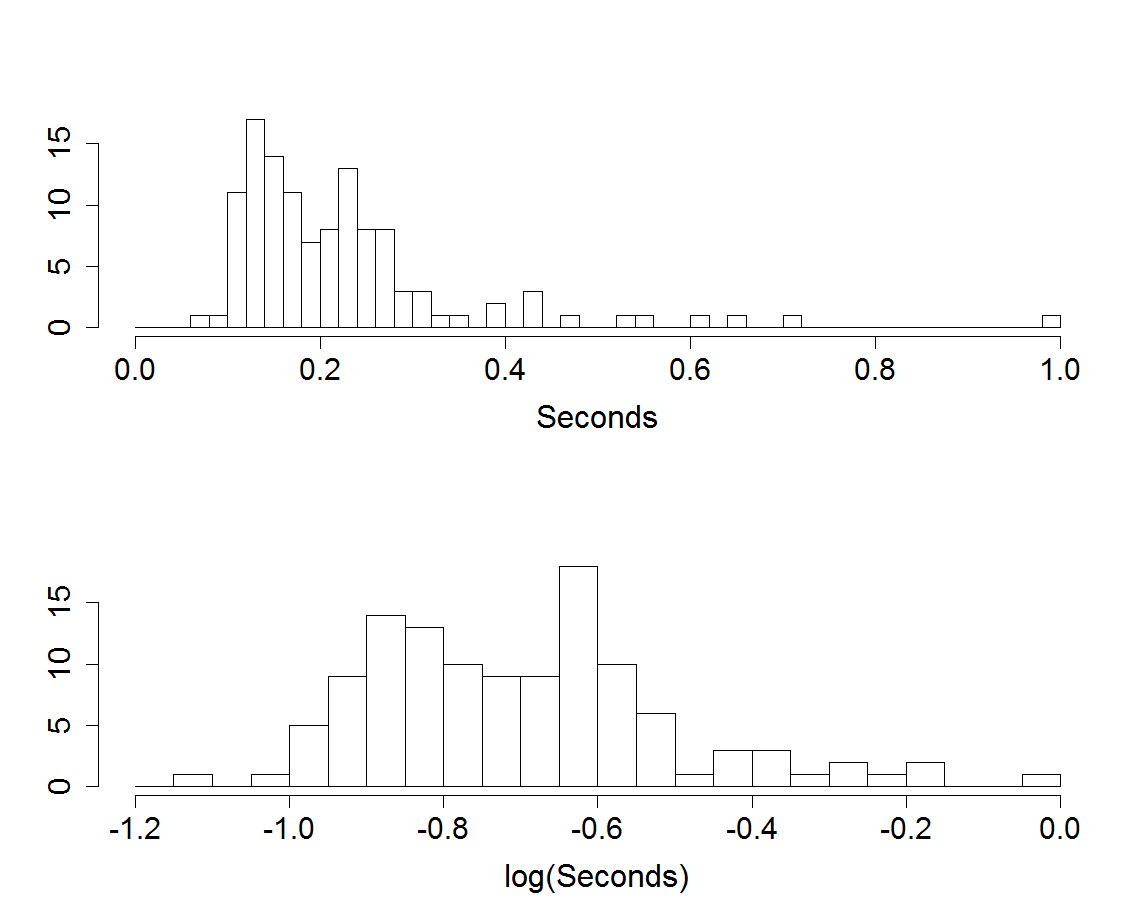 |
Figure 2.3
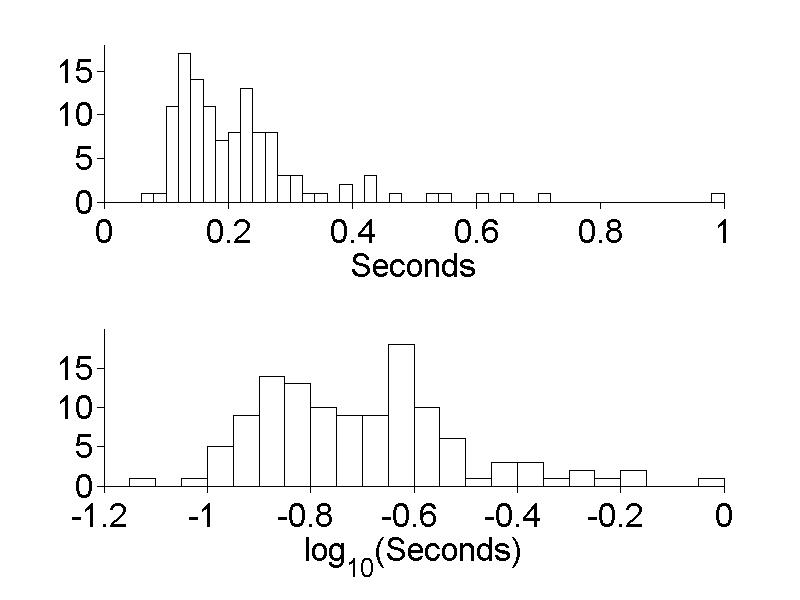 |
3 - Probability and Random Variables
Figure 3.2
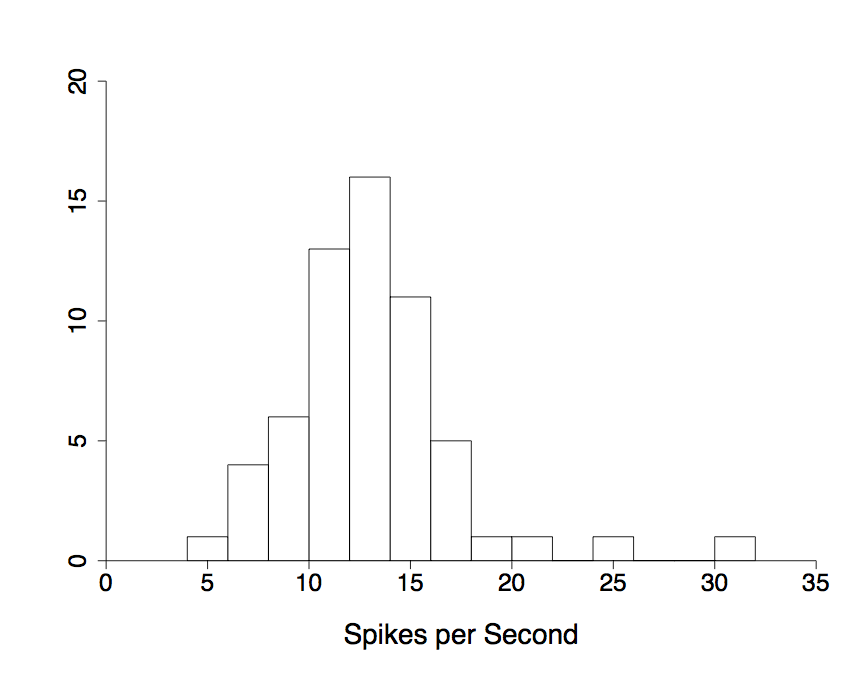 |
 |
|
| |
|
Figure 3.3
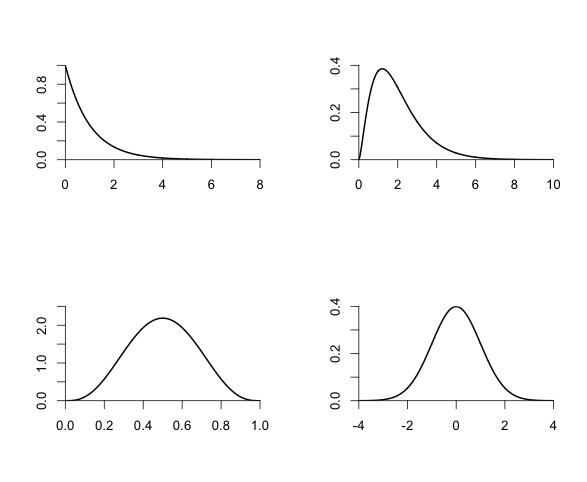 |
 |
|
| |
|
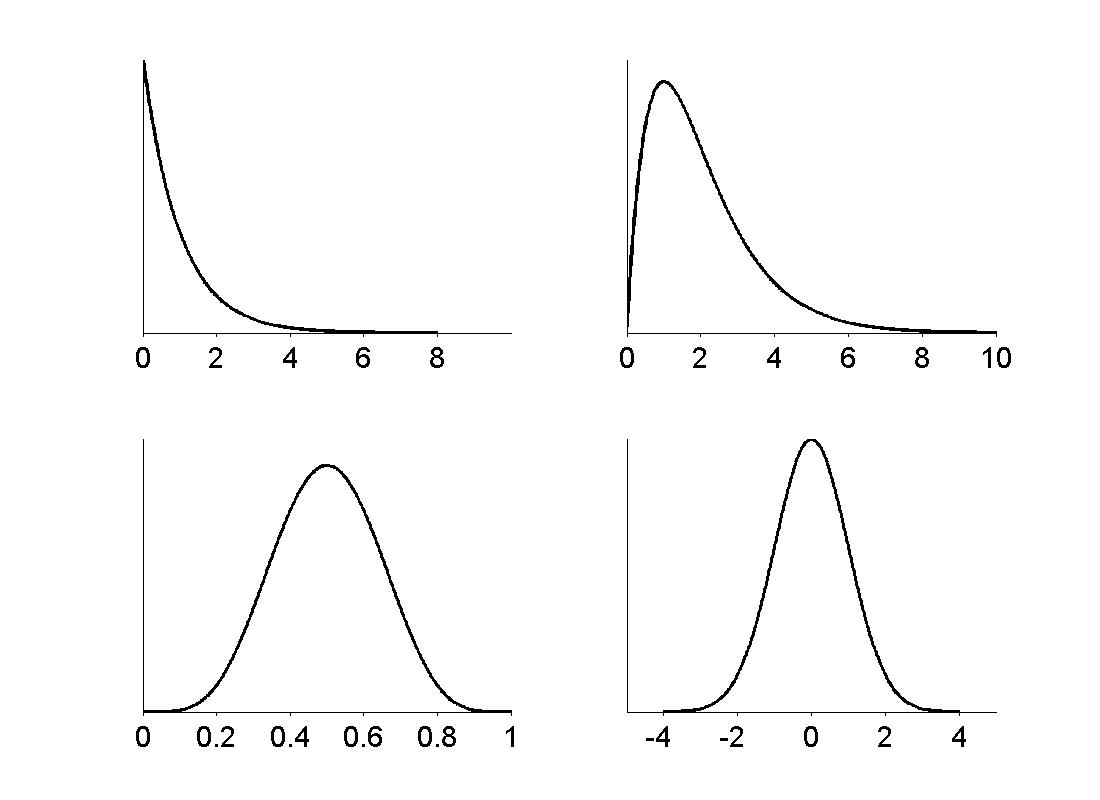
Figure 3.5
 |
 |
|
| |
|
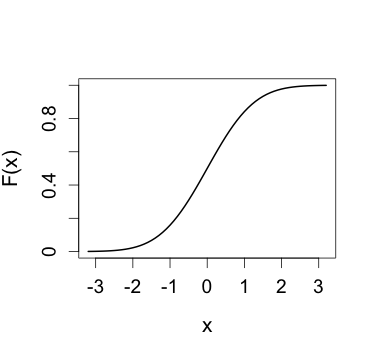
Figure 3.6
 |
 |
|
| |
|
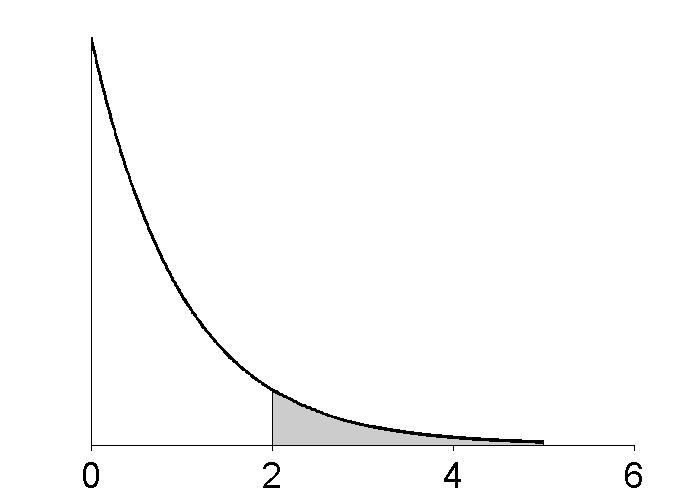
Figure 3.9
 |
 |
|
| |
|
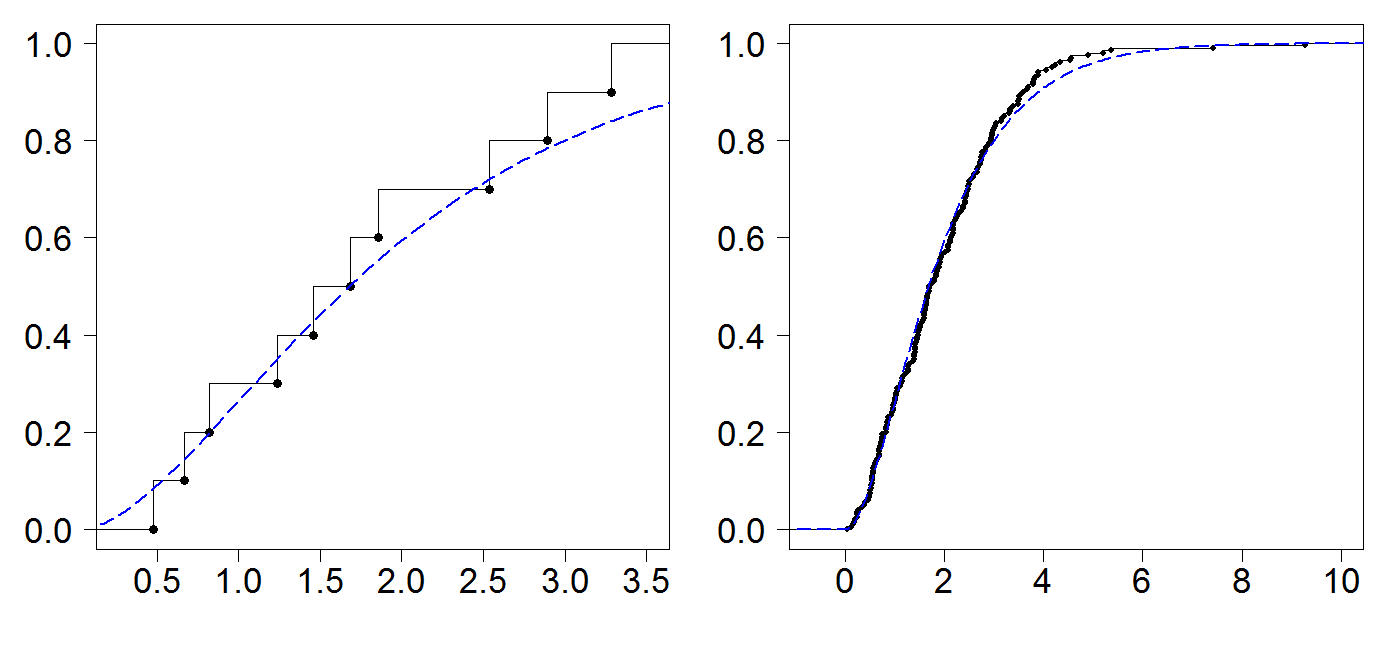
Figure 3.11
 |
 |
|
| |
|
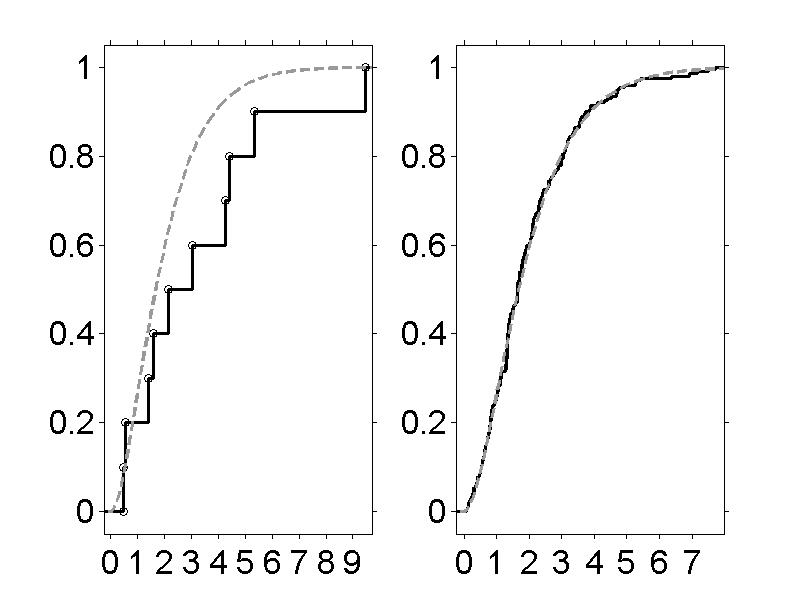
Figure 3.12
 |
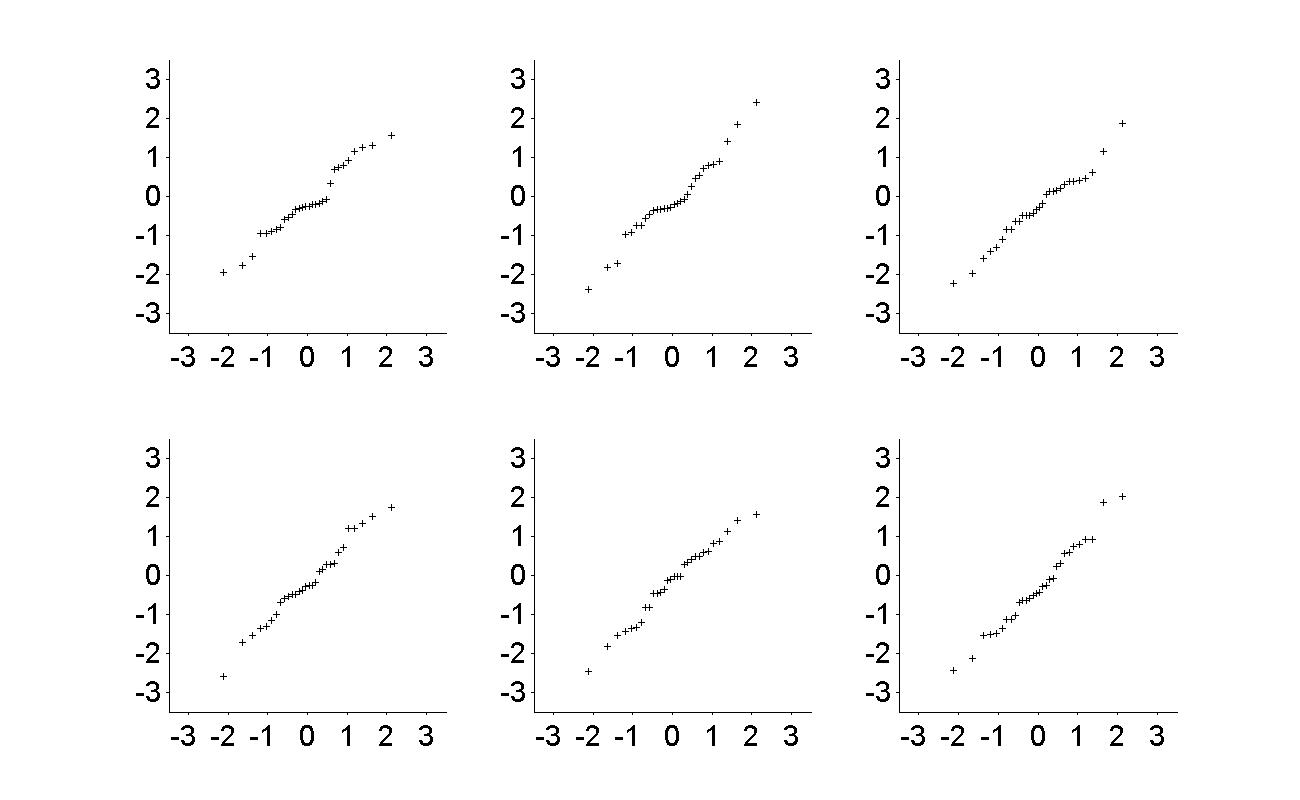 |
|
| |
|
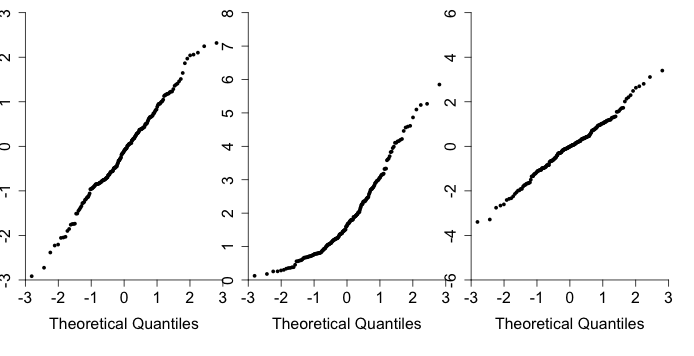
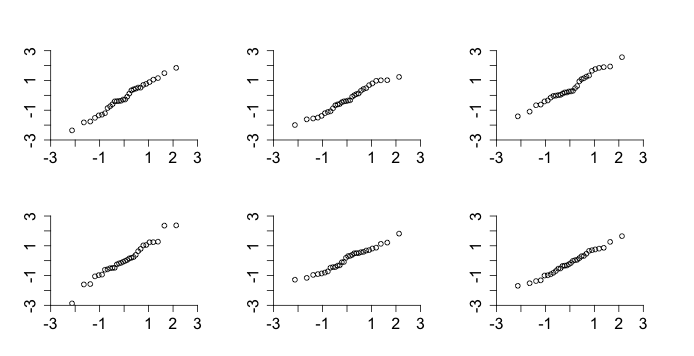
Figure 3.13
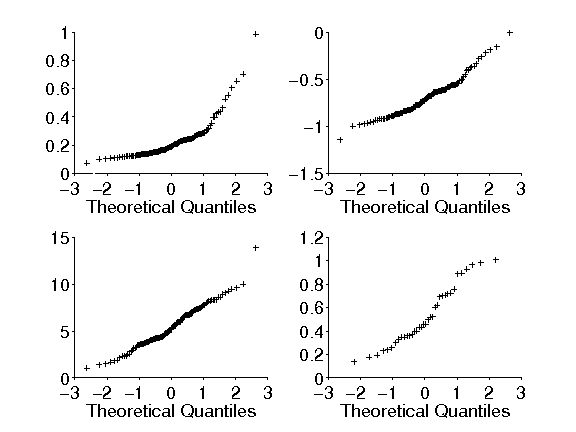 |
4 - Random Vectors
Figure 4.2
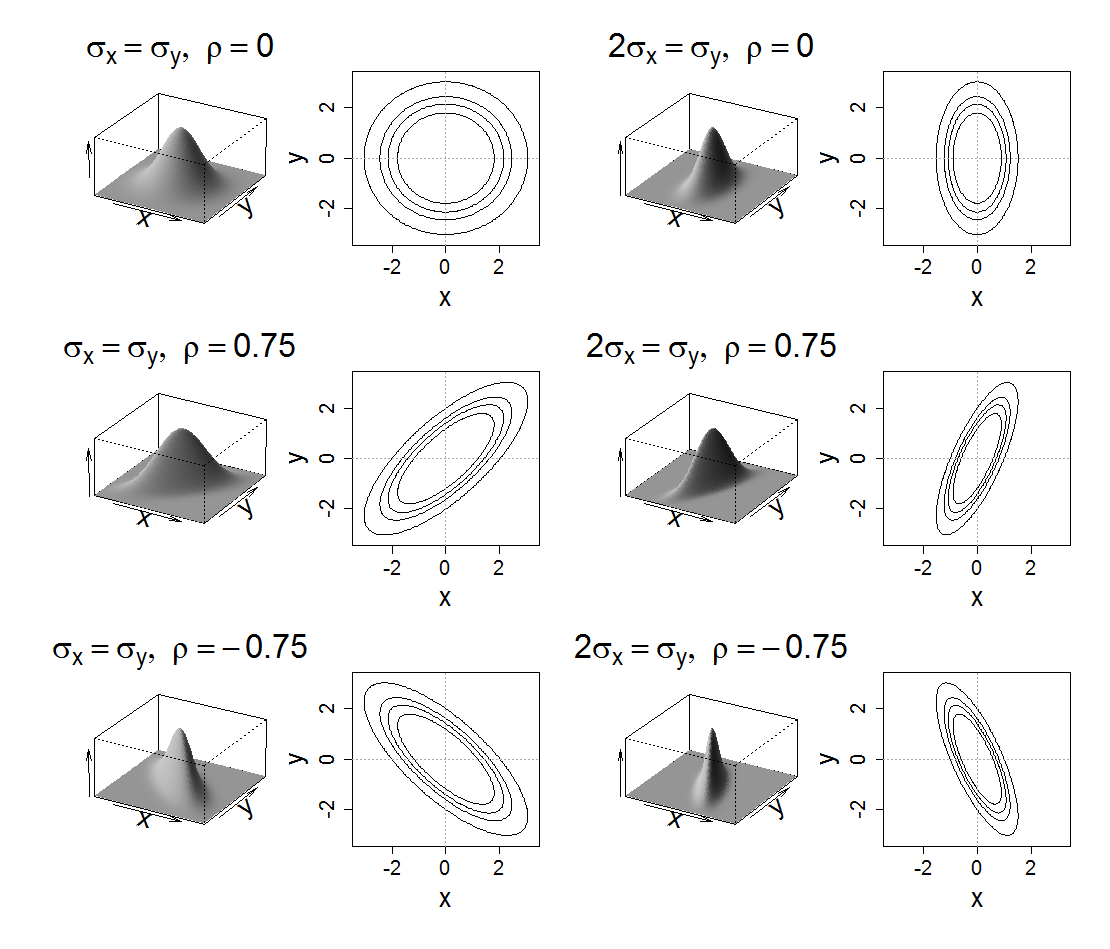 |
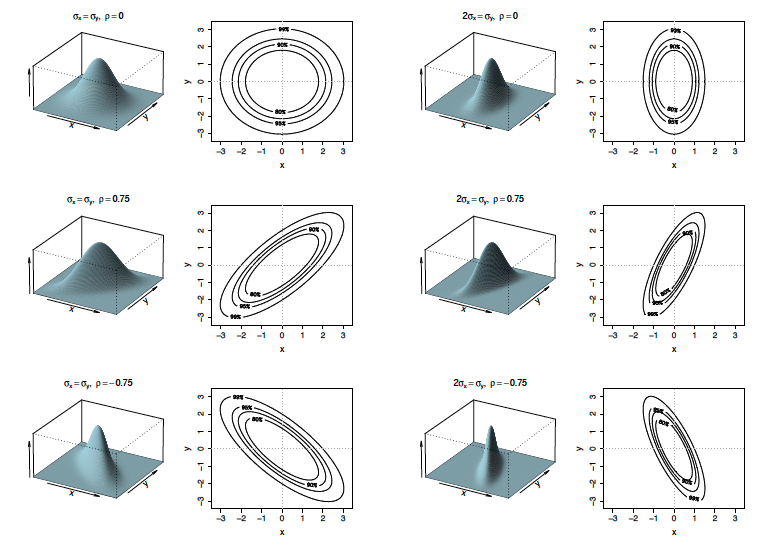 |
|
| |
|
Figure 4.3
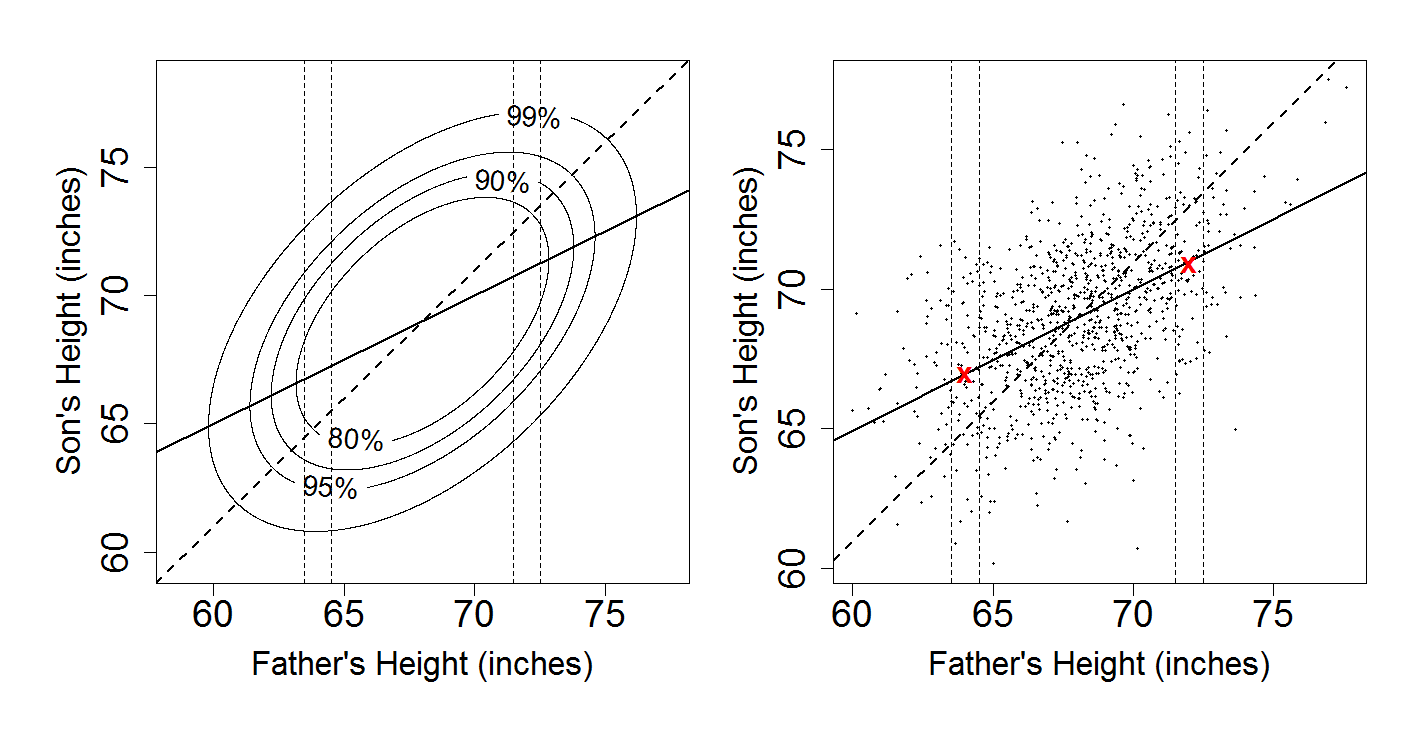 |
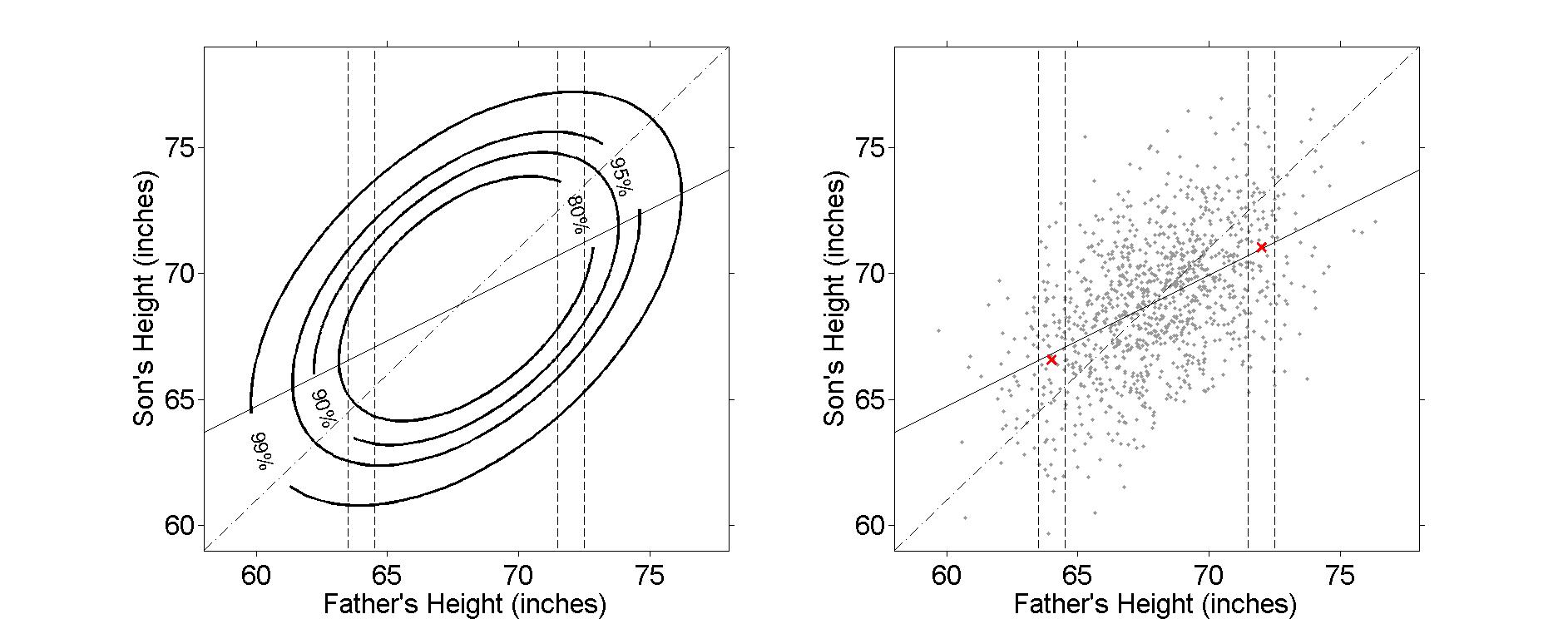 |
|
| |
|
5 - Important Probability Distributions
Figure 5.3
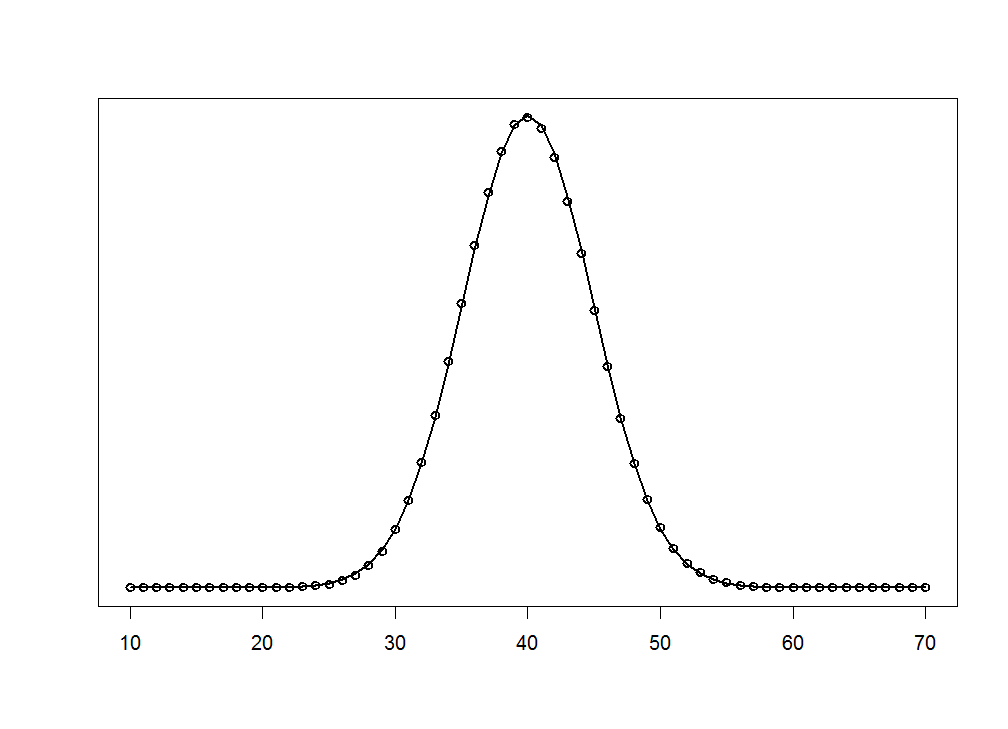 |
 |
|
| |
|
Figure 5.4
 |
 |
|
| |
|
Figure 5.6
 |
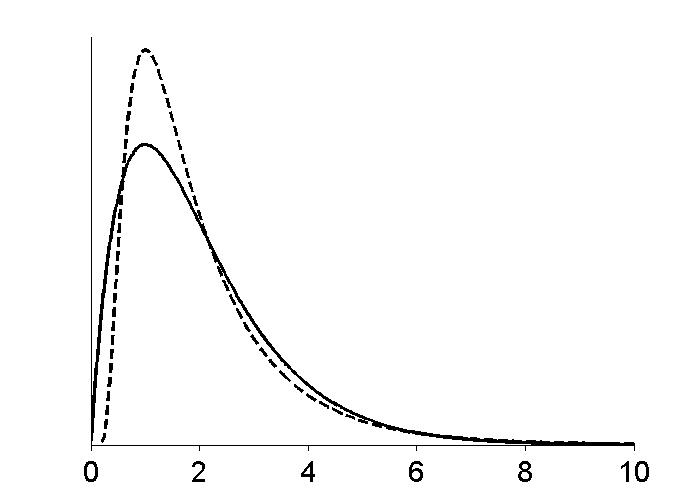 |
|
| |
|
6 - Sequences of Random Variables
Figure 6.1
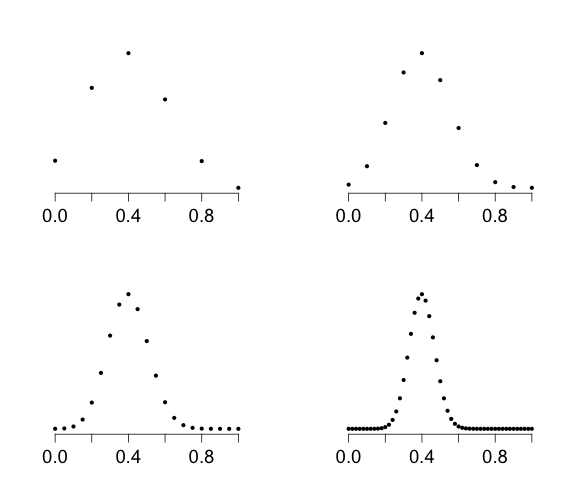 |
 |
|
| |
|
7 - Estimation and Uncertainty
Figure 7.2
 |
 |
|
| |
|
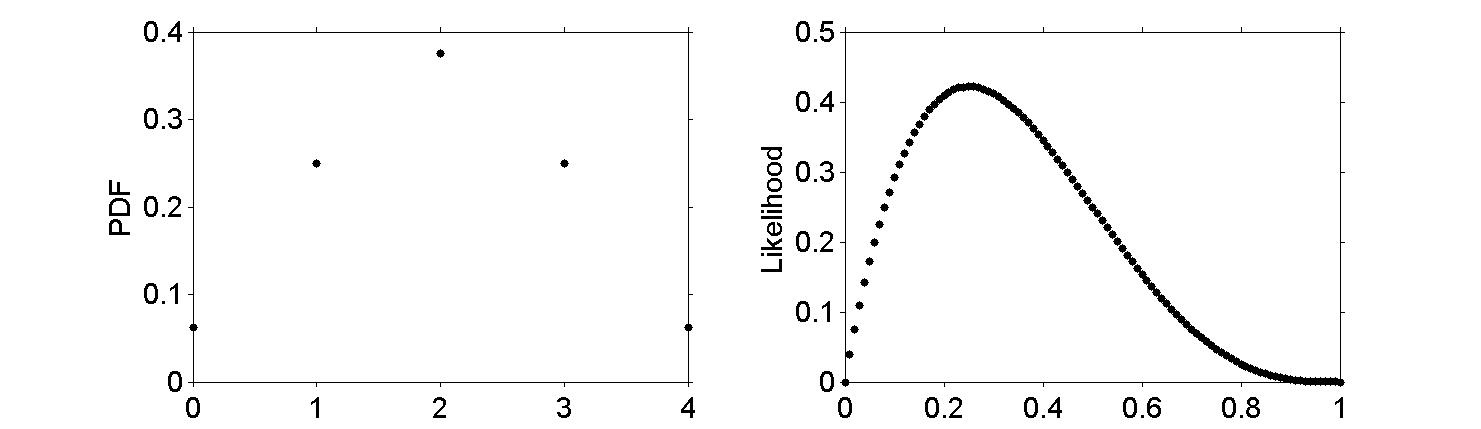
Figure 7.3
 |
8 - Estimation in Theory and in Practice
Figure 8.2
 |
 |
|
| |
|
Figure 8.8
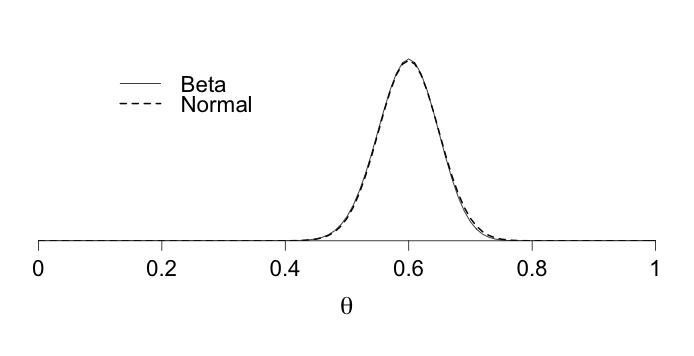 |
 |
|
| |
|
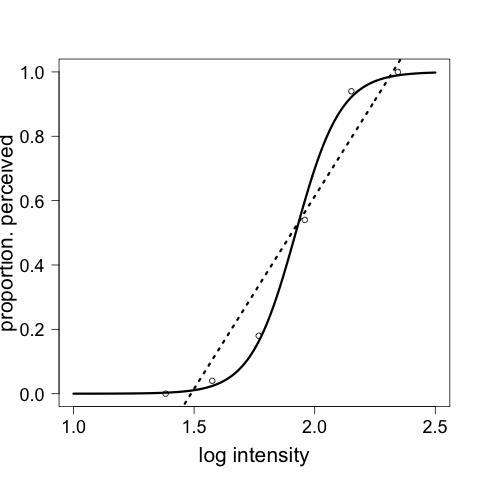
Figure 8.9
 |
9 - Propagation of Uncertainty and the Bootstrap
Figure 9.1
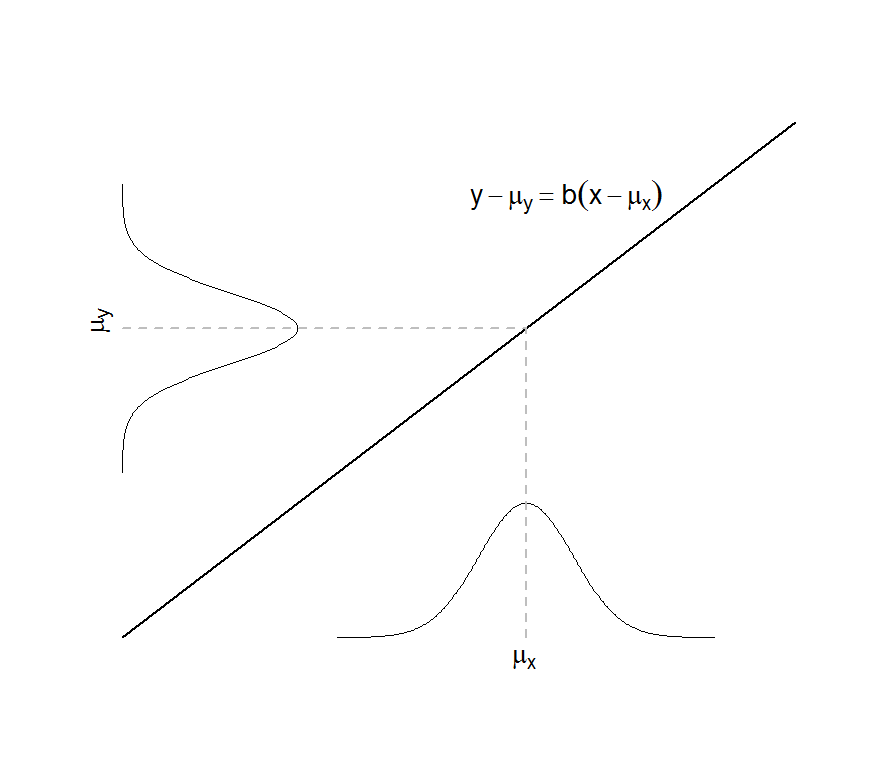 |
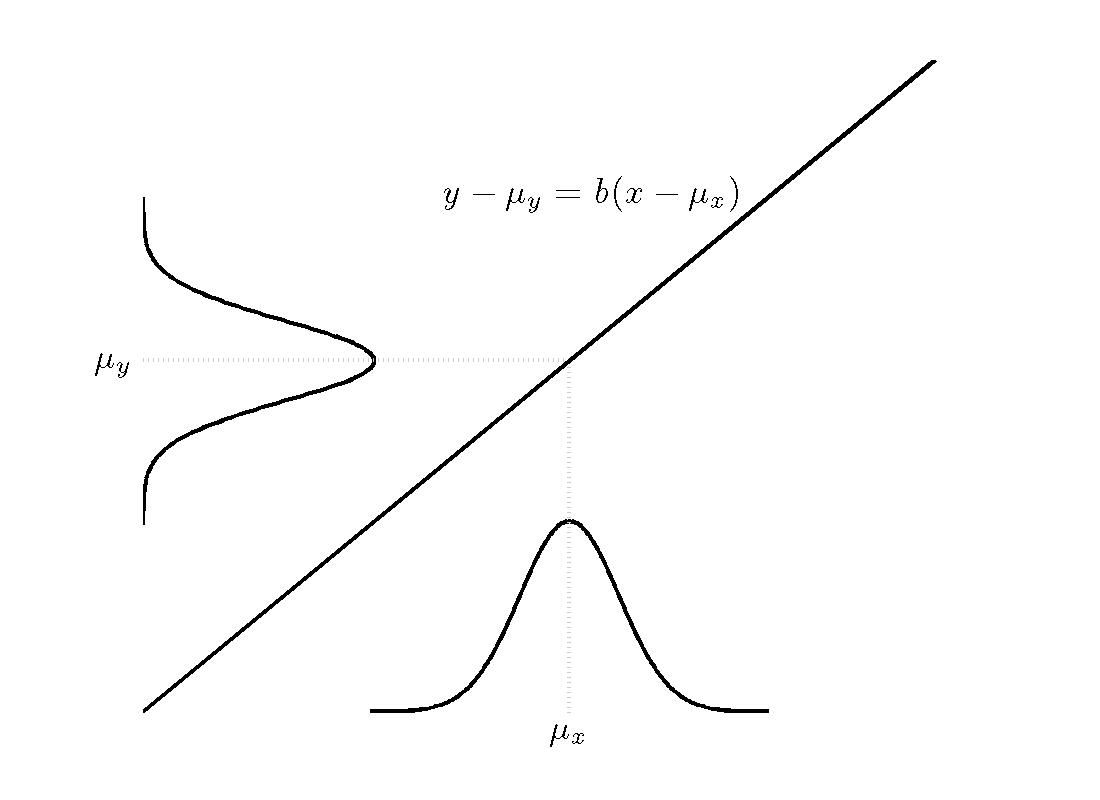 |
|
| |
|
Figure 9.2
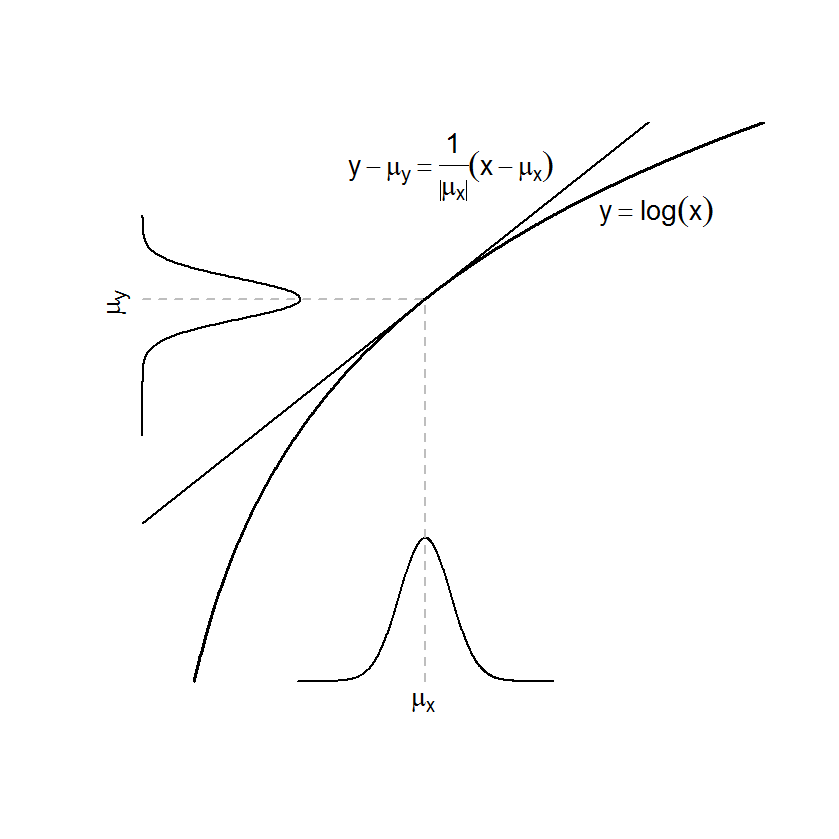 |
 |
|
| |
|
10 - Models, Hypotheses, and Statistical Significance
Figure 10.1
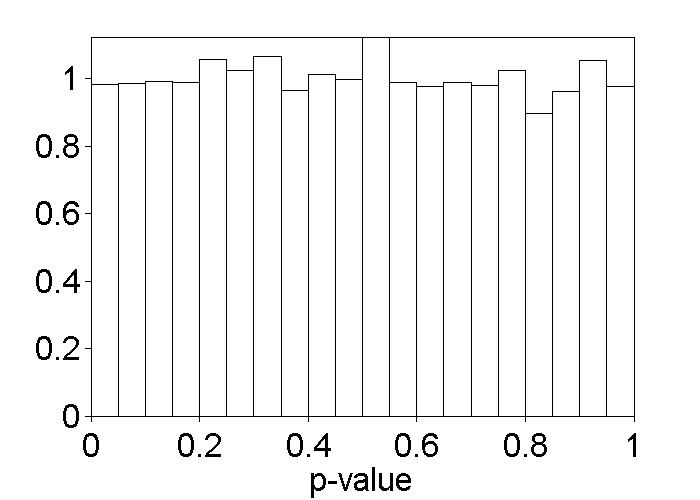 |
Figure 10.3
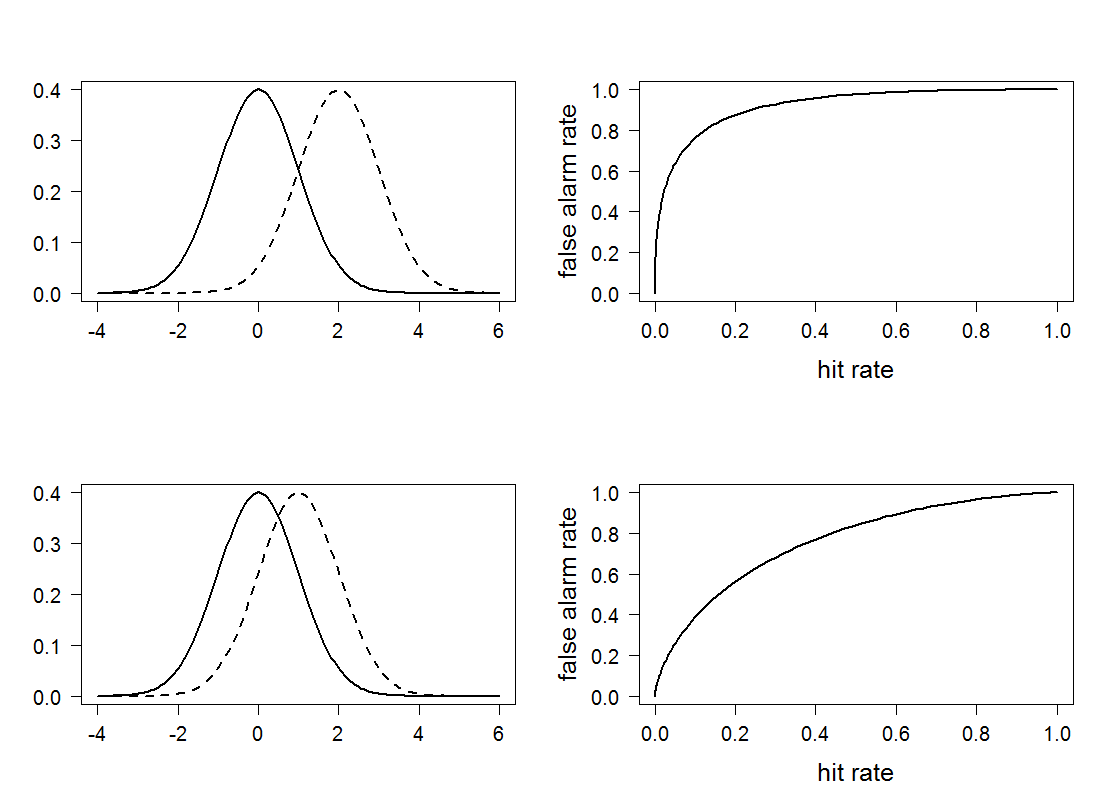 |
 |
|
| |
|
11 - General Methods for Testing Hypotheses
12 - Linear Regression
Figure 12.2
 |
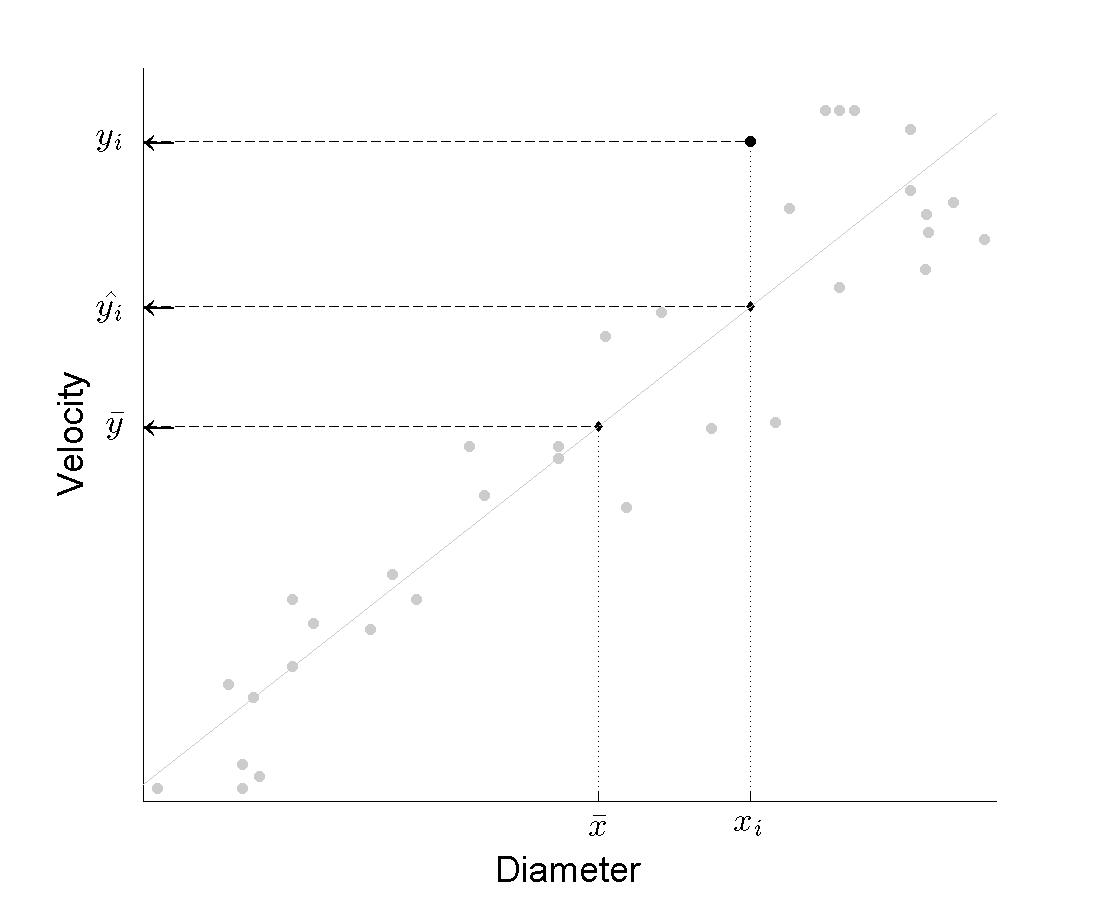 |
|
| |
|
Figure 12.5
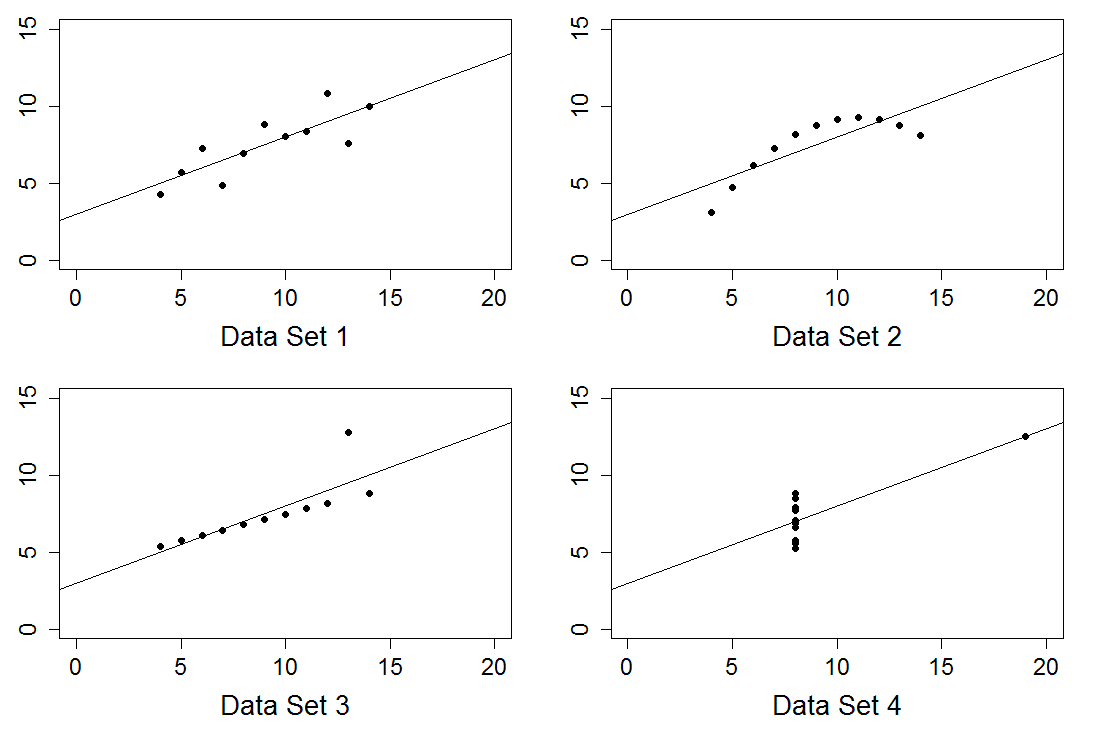 |
 |
|
| |
|
Figure 12.6
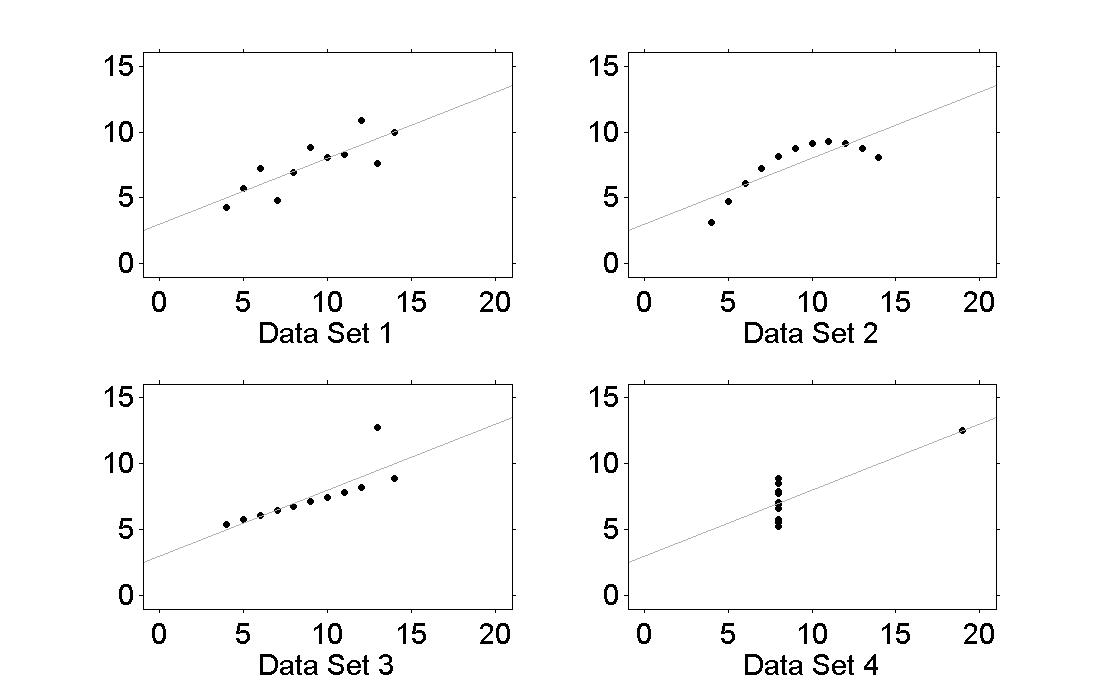
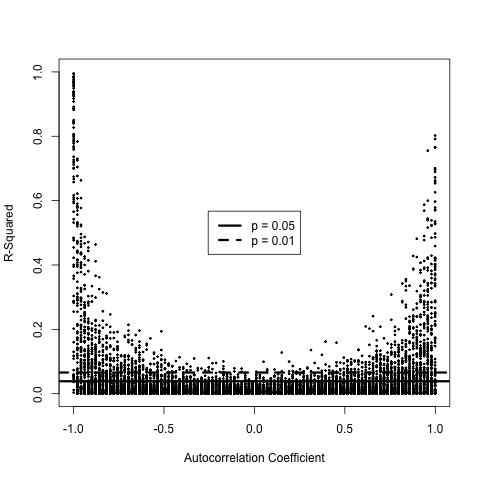 |
Figure 12.7
 |
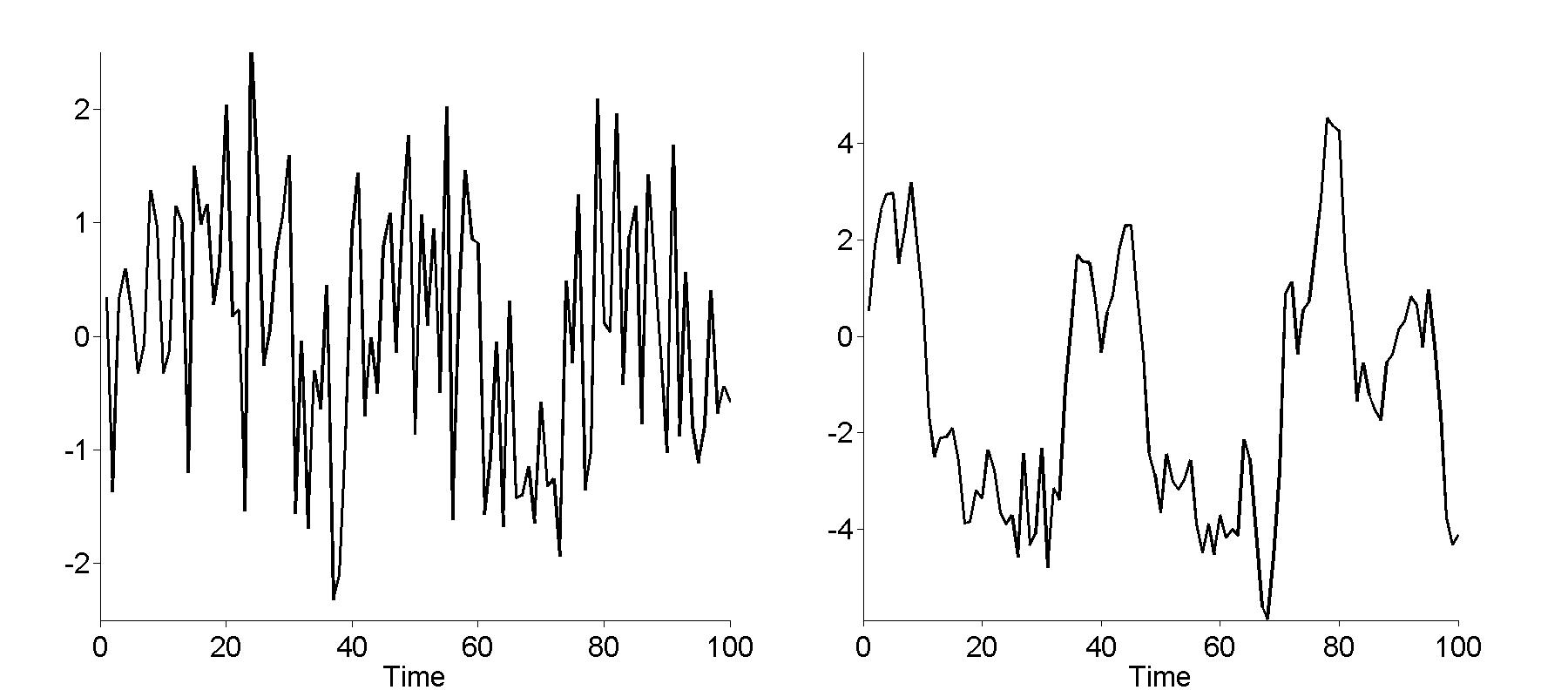 |
|
| |
|
13 - Analysis of Variance
14 - Generalized Linear and Nonlinear Regression
Figure 14.1
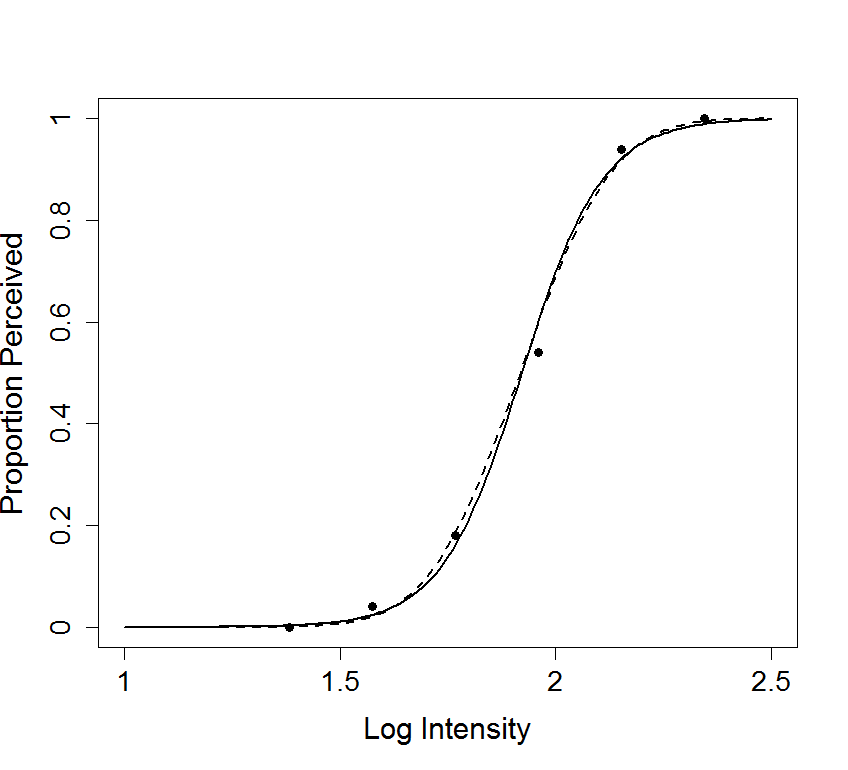 |
 |
|
| |
|
Figure 14.4
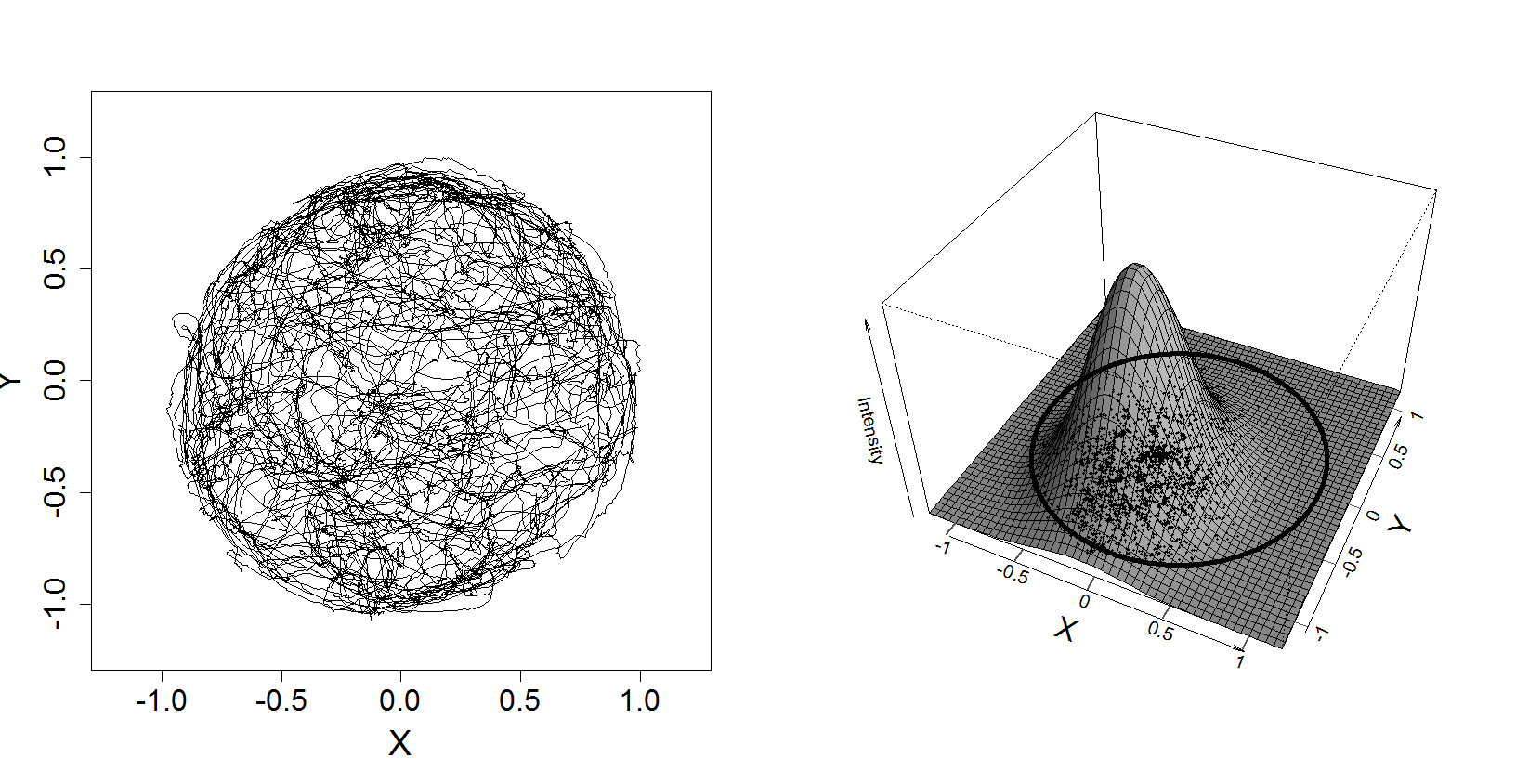 |
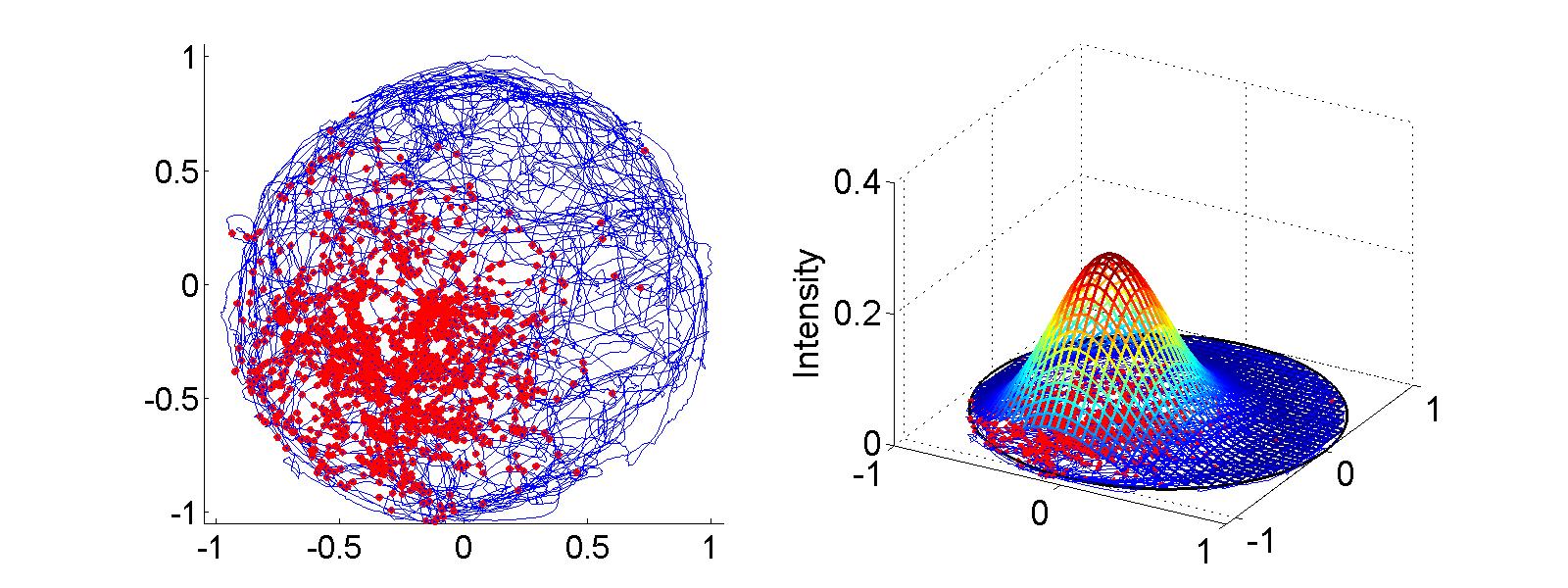 |
|
| |
|
15 - Nonparametric Regression
Figure 15.2
 |
 |
|
| |
|
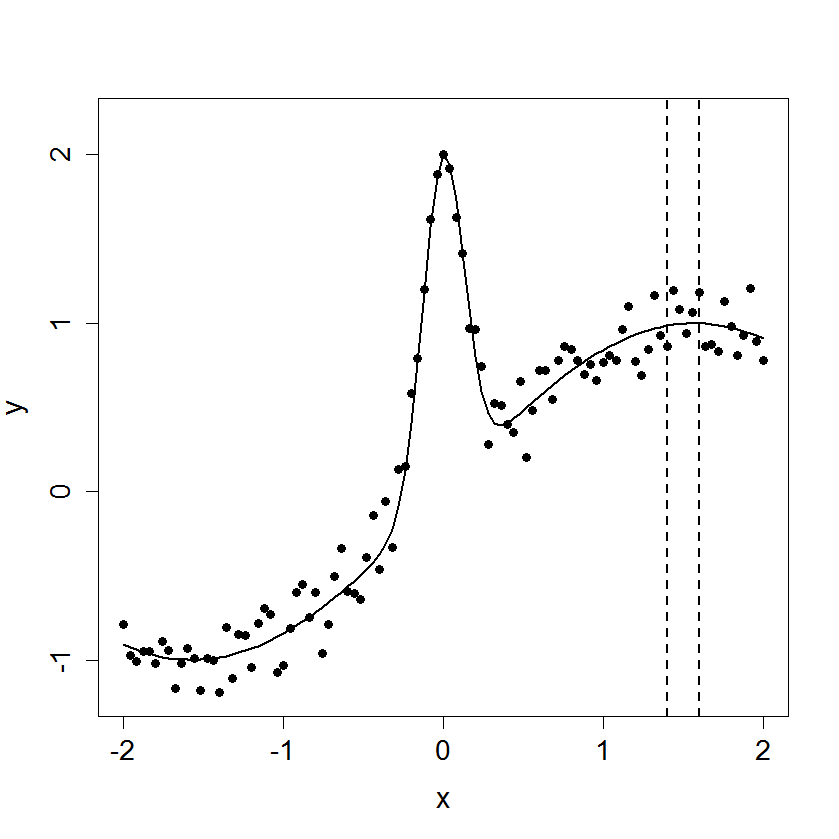
Figure 15.4
 |
 |
|
| |
|
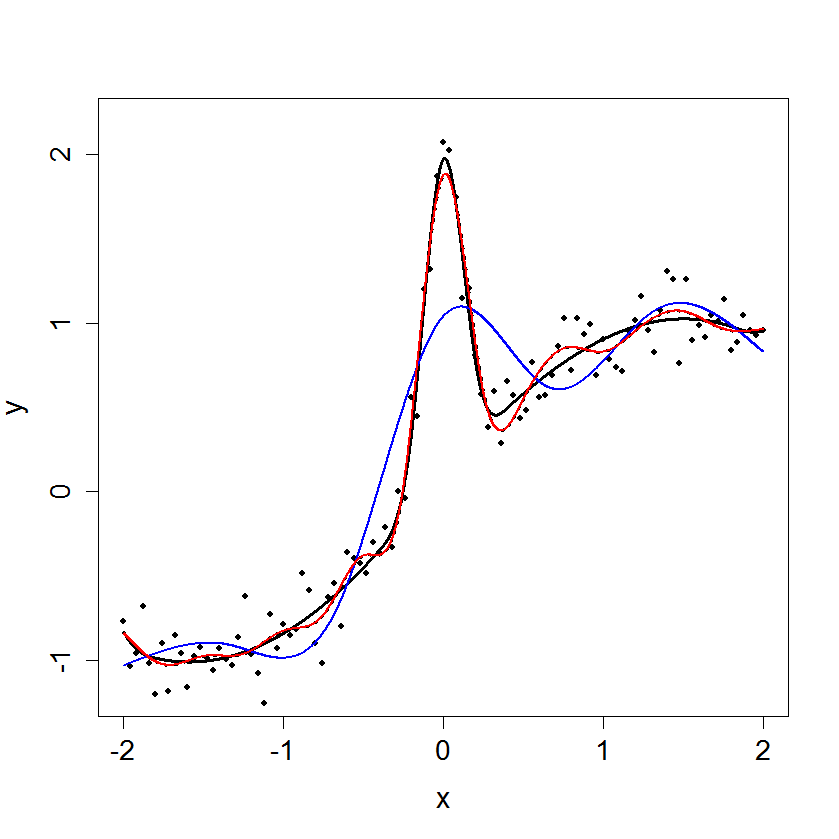
Figure 15.6
 |
 |
|
| |
|
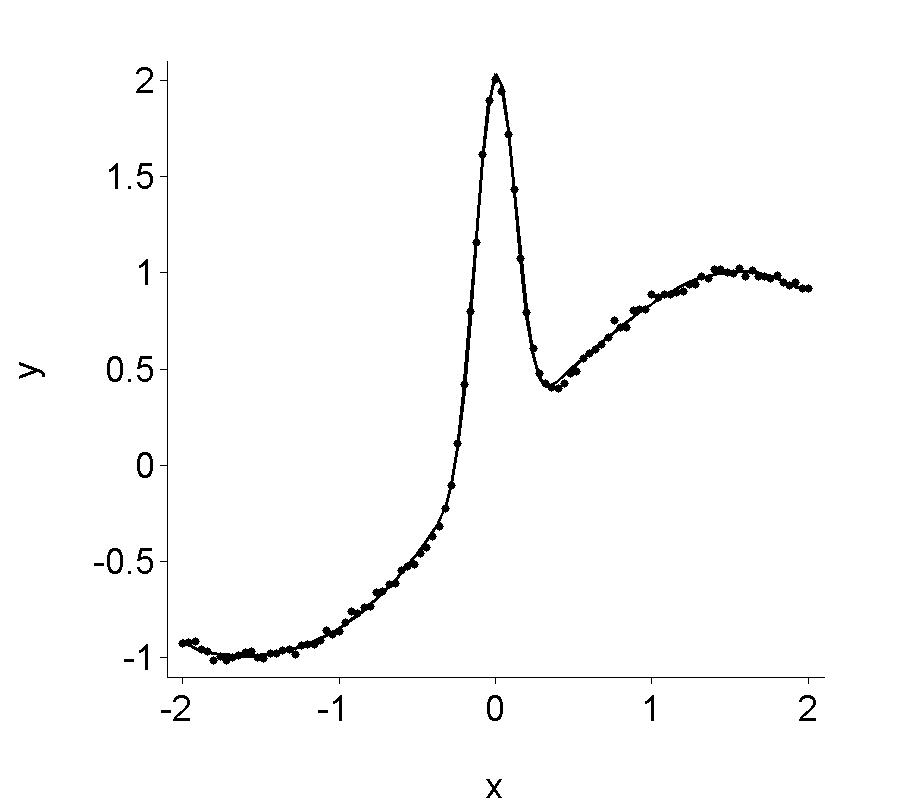
Figure 15.12
 |
 |
|
| |
|
16 - Bayesian Methods
17 - Multivariate Analysis
18 - Time Series
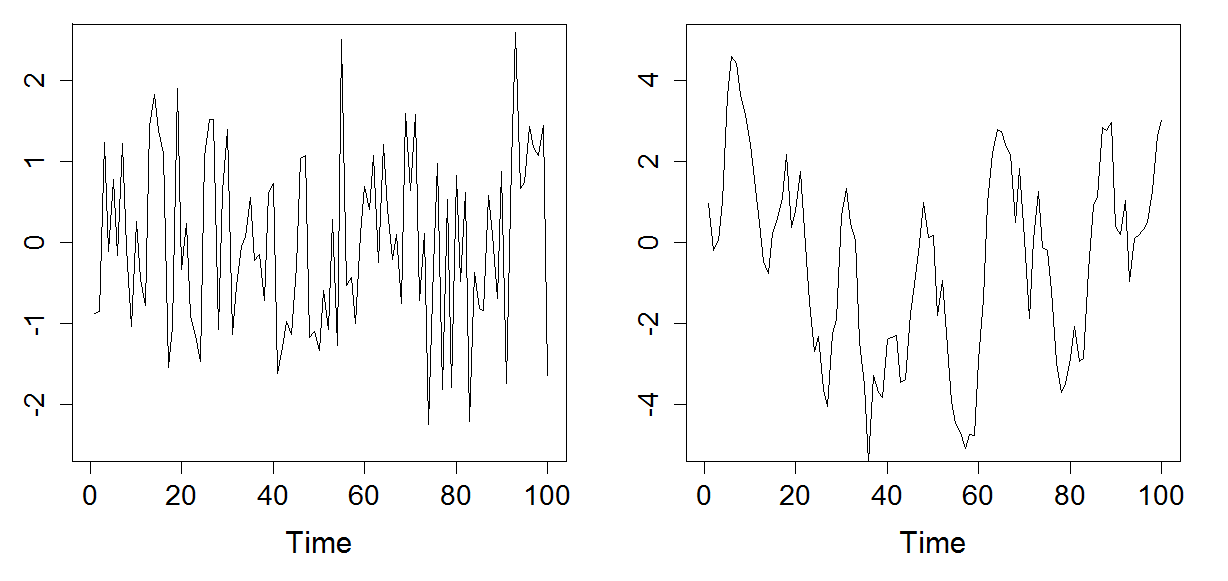
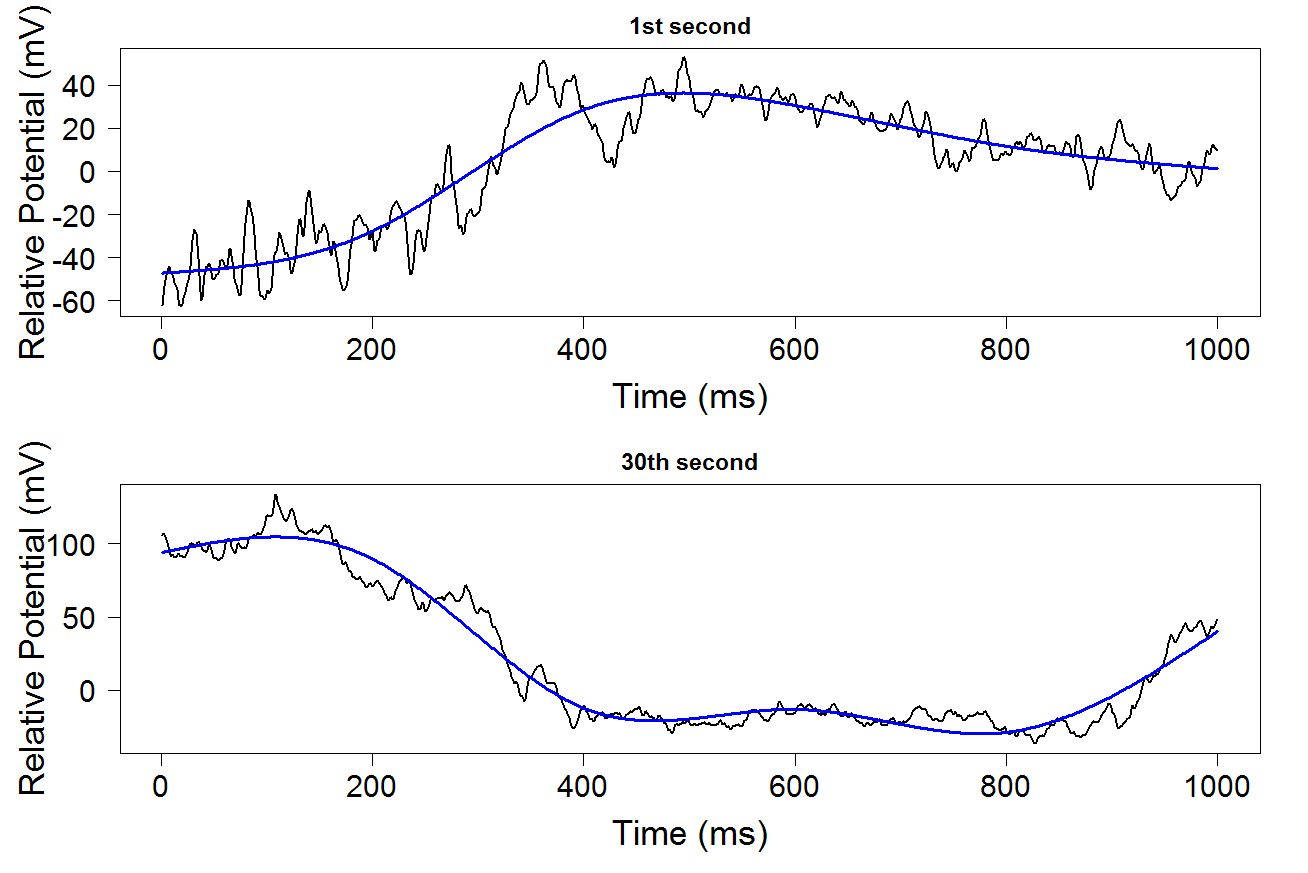
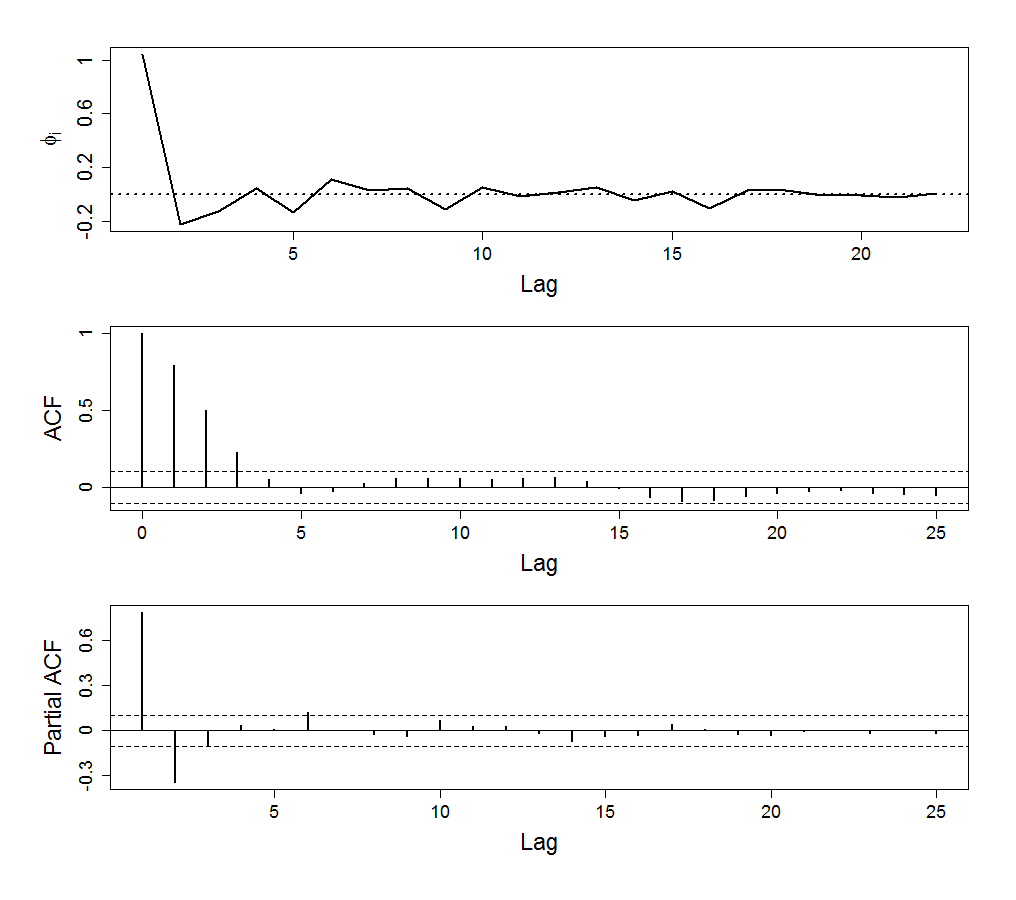
Figure 18.1
 |
 |
|
| |
|
Figure 18.1
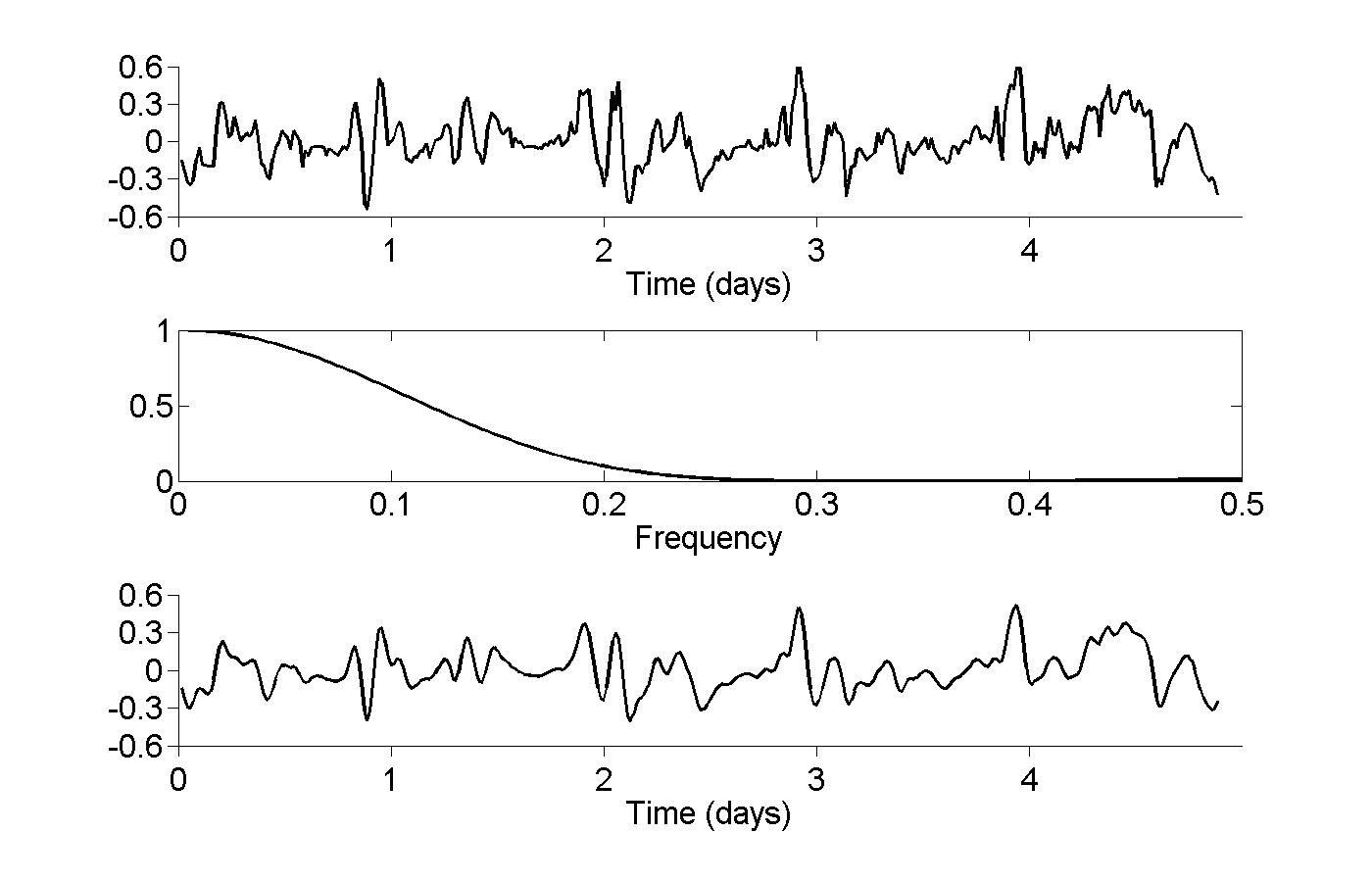 |
Figure 18.2
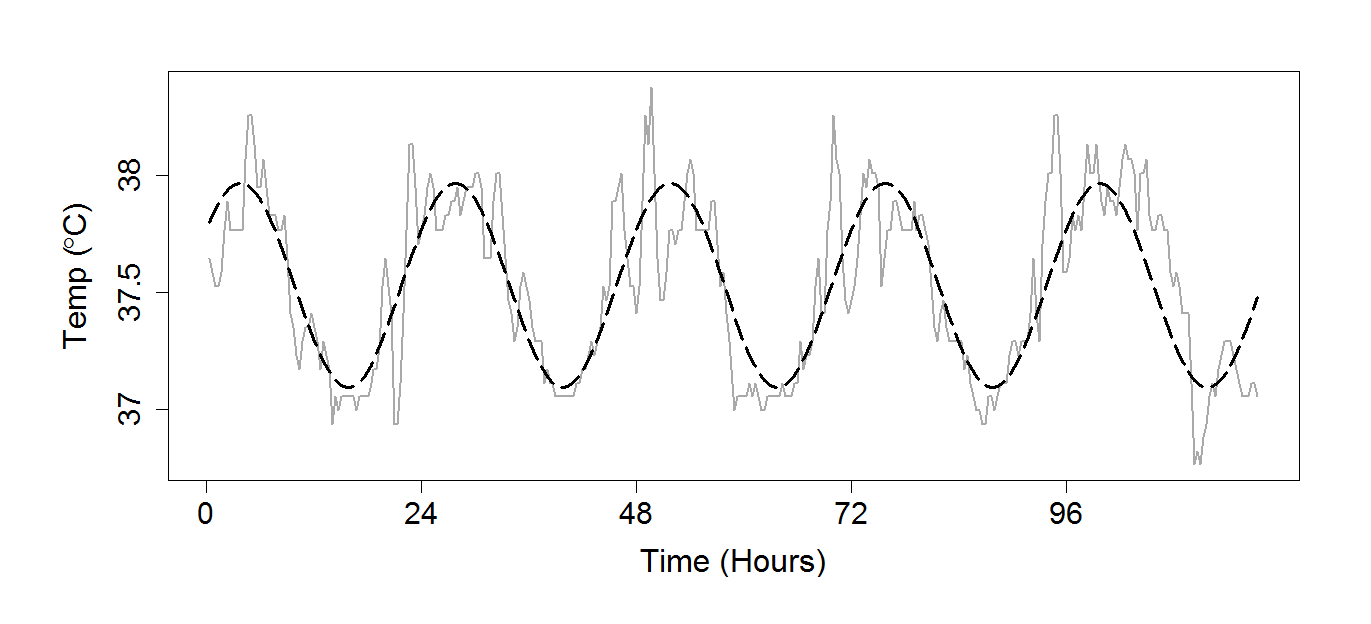 |
 |
|
| |
|
Figure 18.3
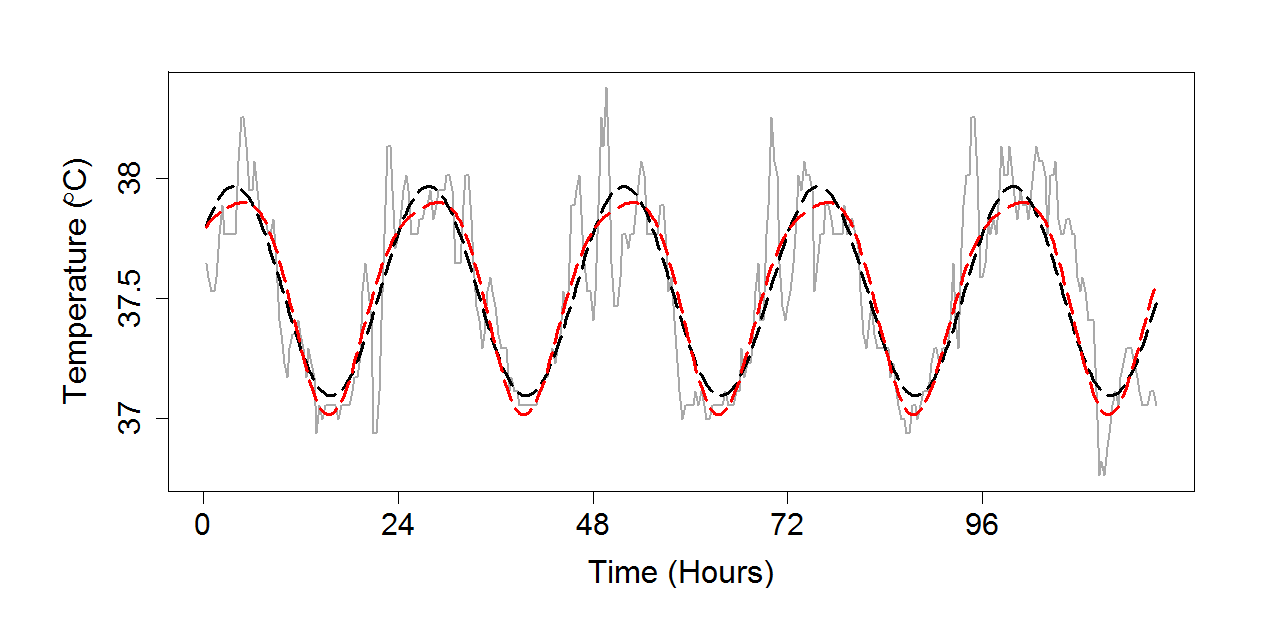 |
 |
|
| |
|
Figure 18.4
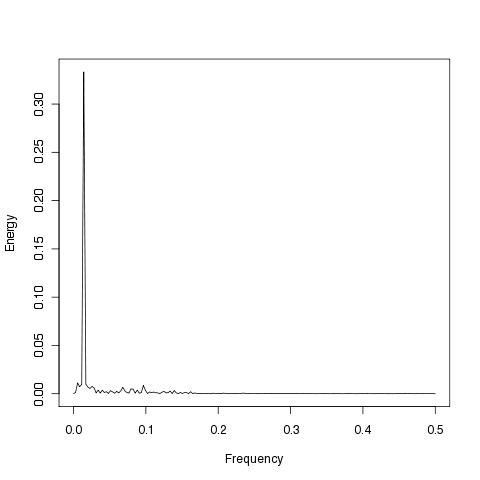 |
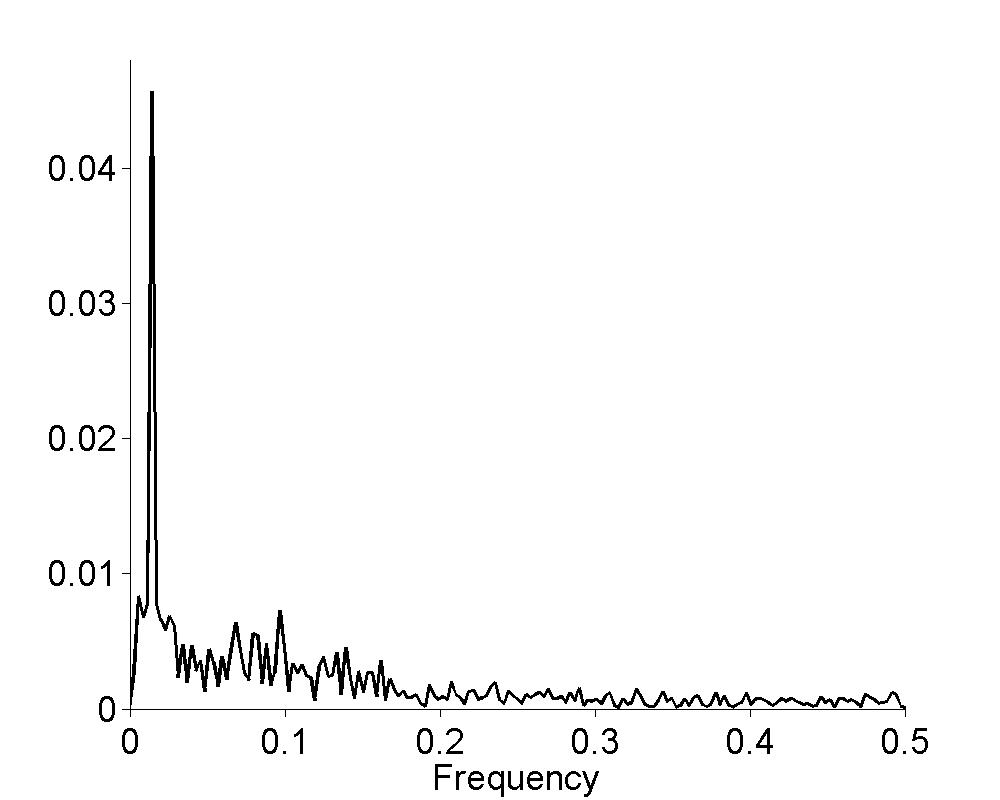 |
|
| |
|
Figure 18.5
 |
 |
|
| |
|
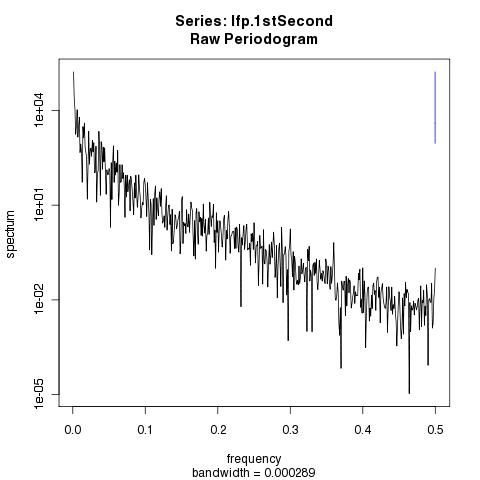
Figure 18.6
 |
 |
|
| |
|
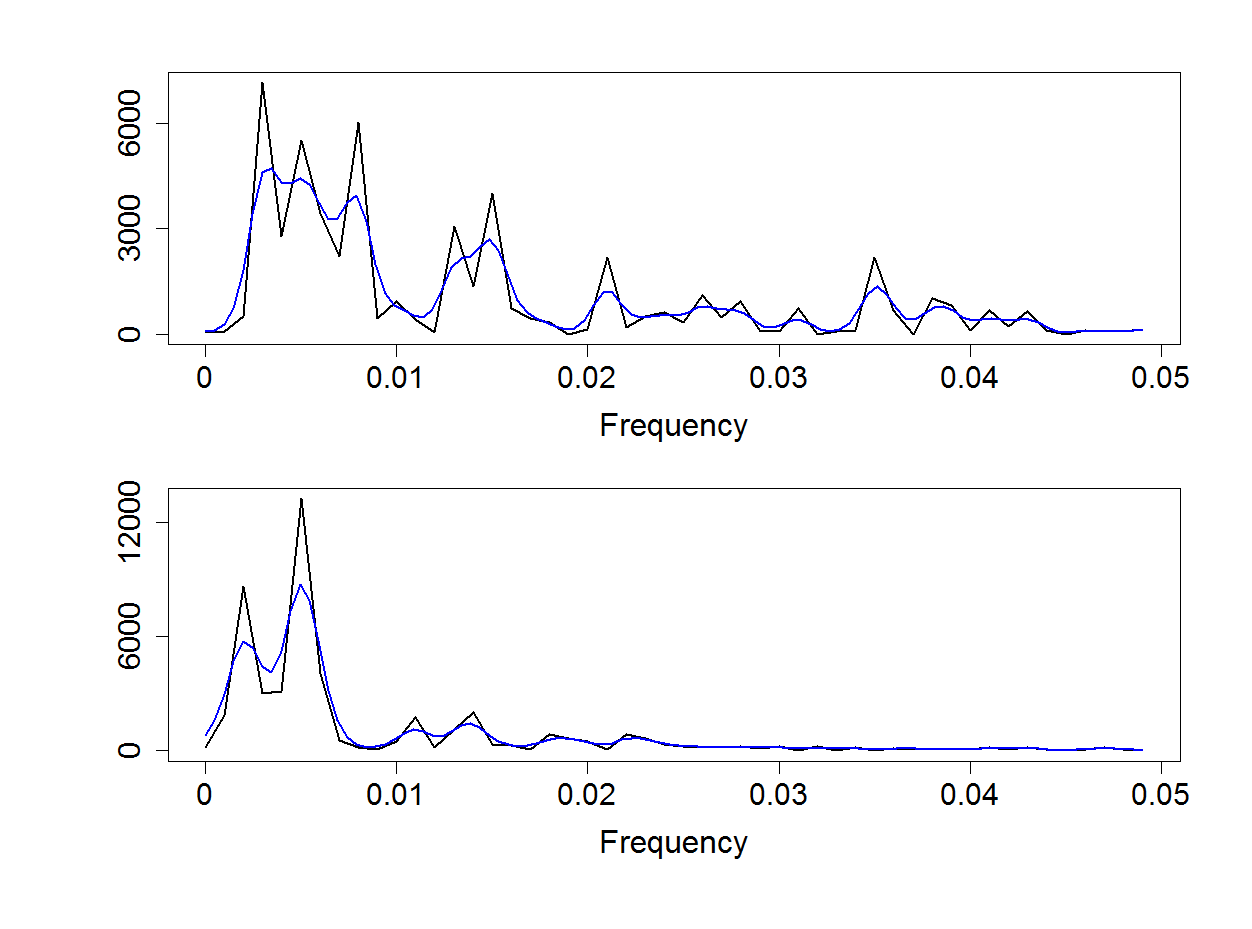
Figure 18.7
 |
 |
|
| |
|
Figure 18.8
 |
 |
|
| |
|
Figure 18.11
 |
 |
|
| |
|
Figure 18.12
 |
 |
|
| |
|
Figure 18.13
 |
 |
|
| |
|
Figure 18.14
 |
 |
|
| |
|
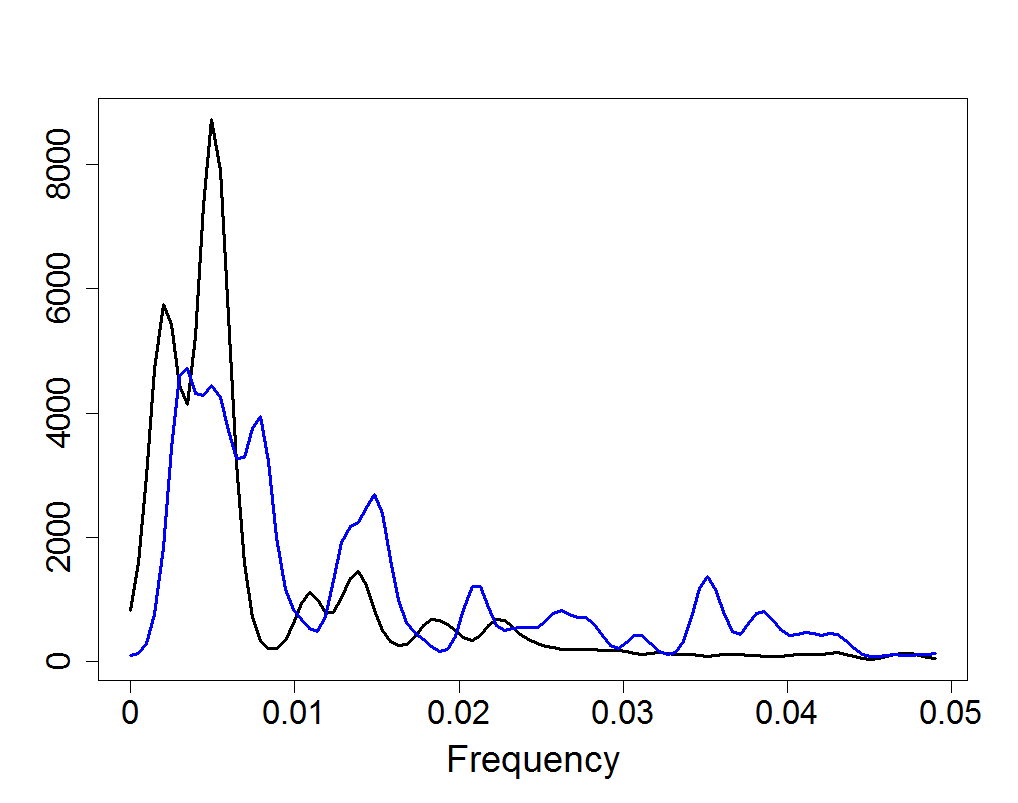
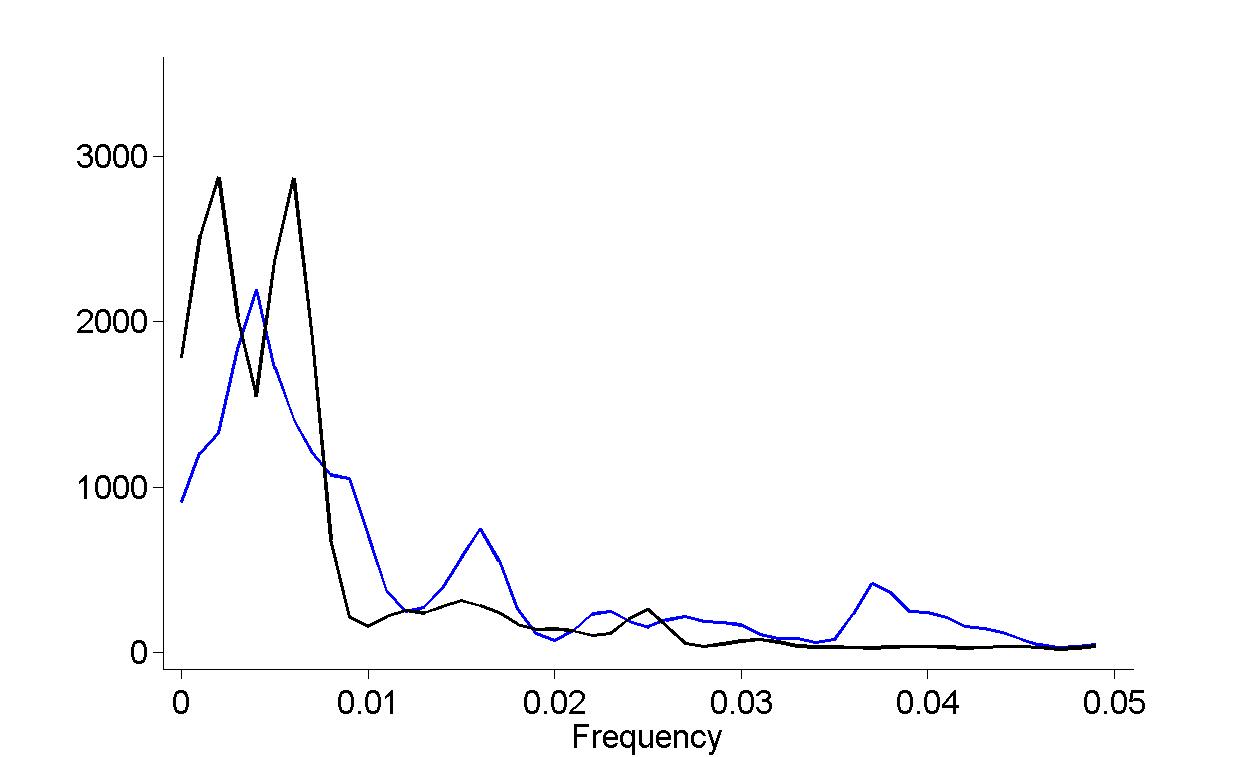
Figure 18.15
 |
 |
|
| |
|
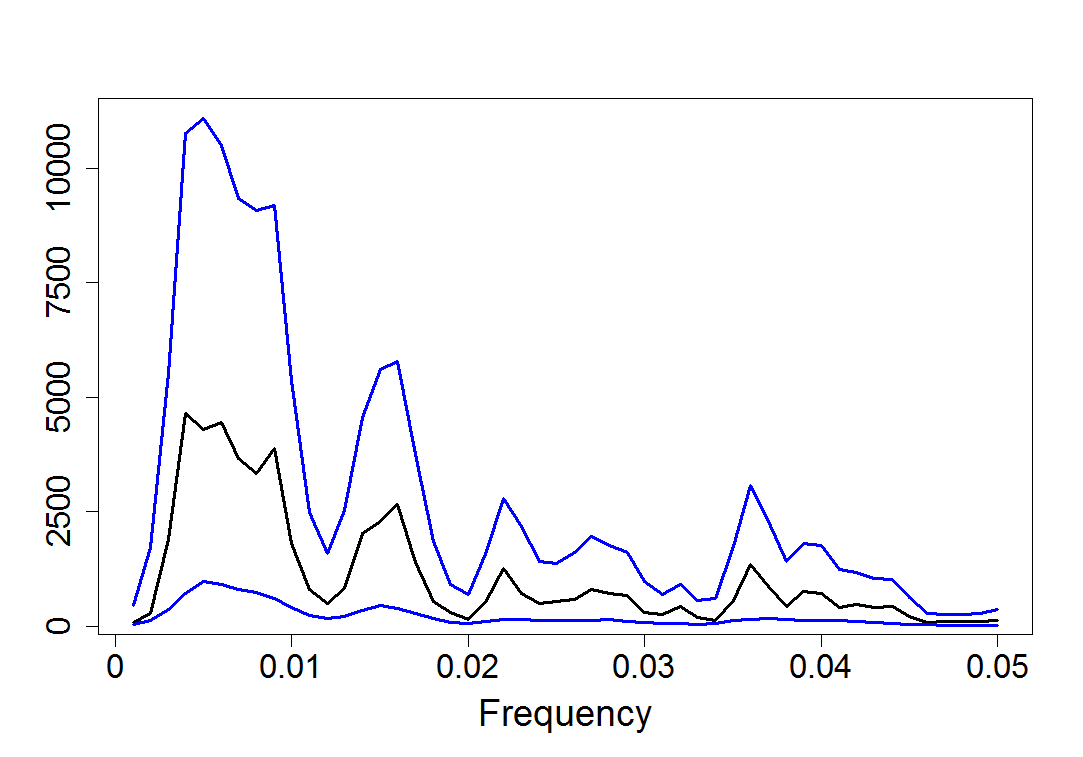
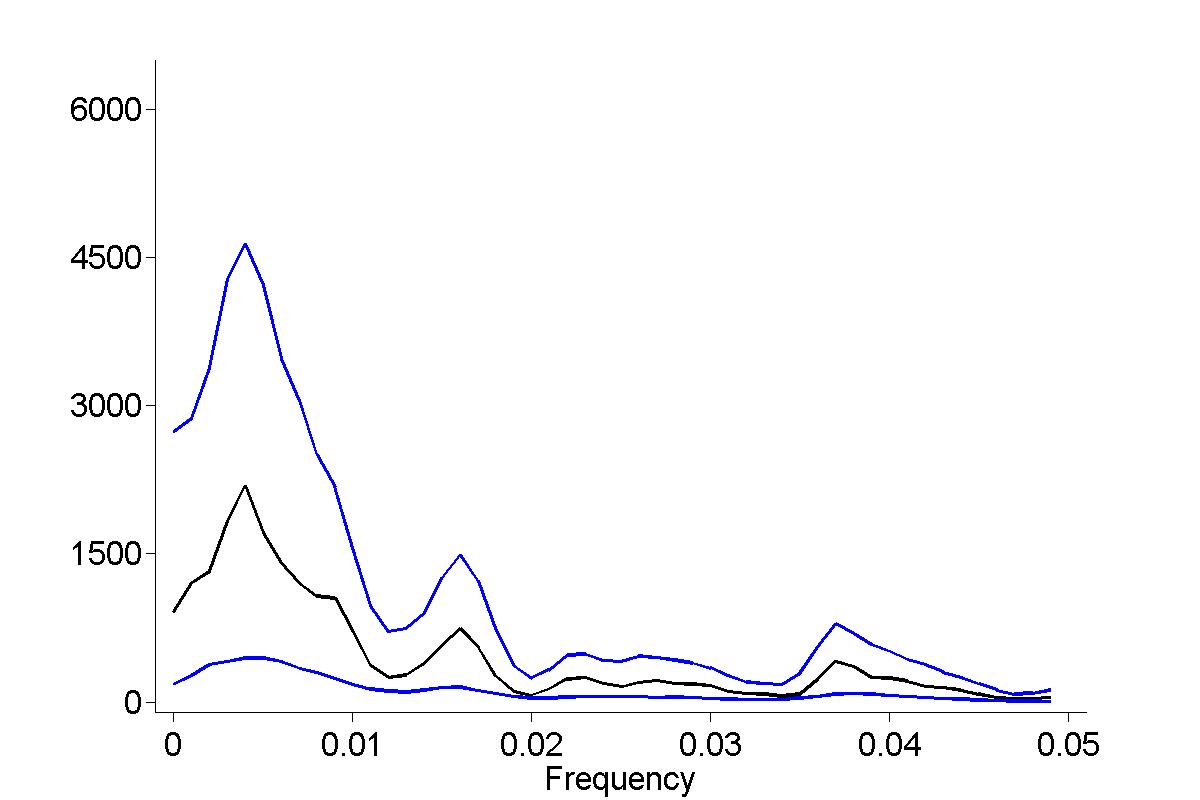
Figure 18.16
 |
 |
|
| |
|
19 - Point Processes
Figure 19.9
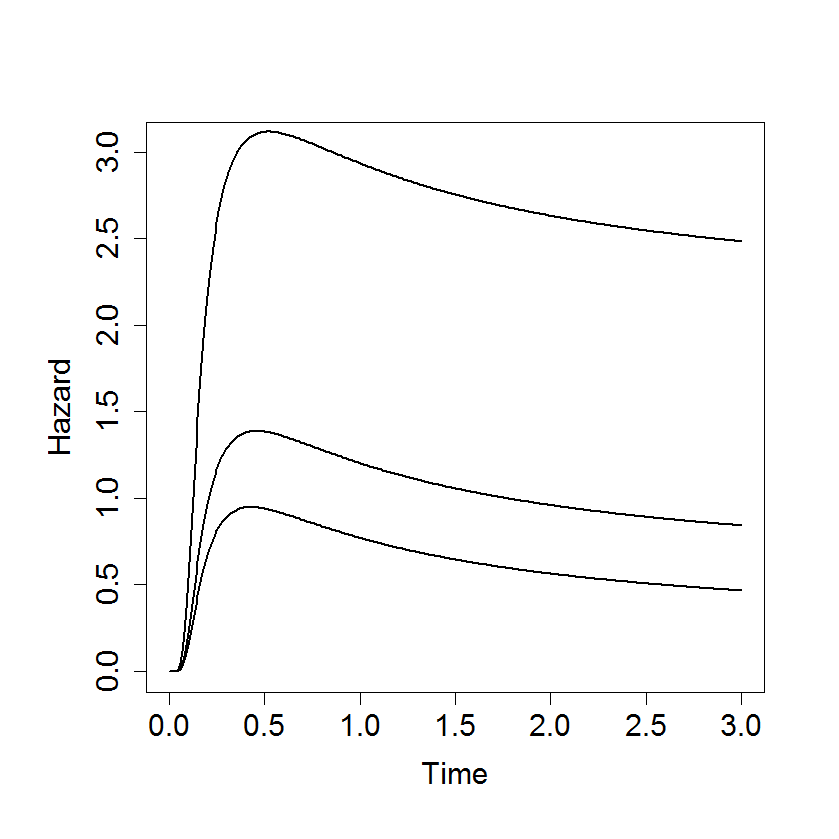 |
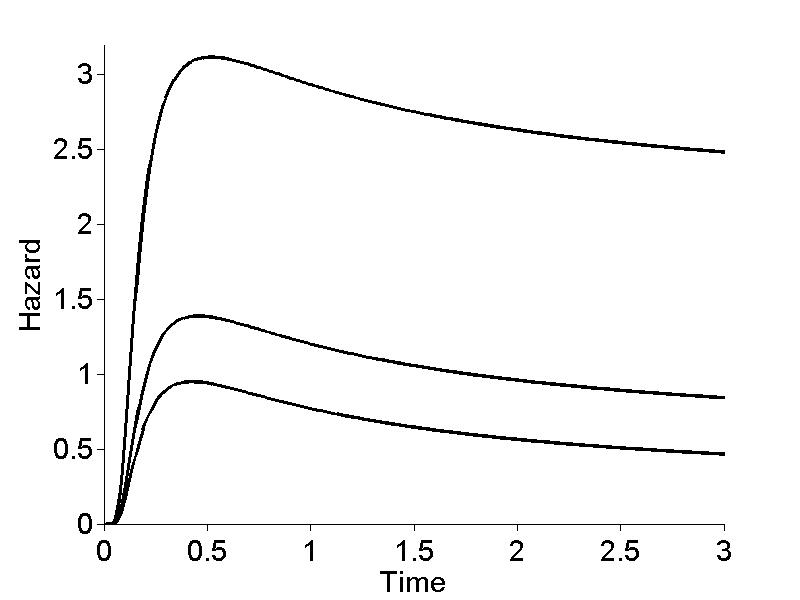 |
|
| |
|
Book: Geometrical Foundations of Asymptotic Inference
by Robert E. Kass and Paul Vos

Review from the Journal of the American Statistical Association, 94: 646, 1999 by Bruce G. Lindsay, Pennsylvania State University:
This book tackles one of the most mathematically challenging subjects in statistics: application of differential geometry to the study of asymptotic inference. It provides a review and synthesis of some of the most important work in this area, with a genuine attempt to make it as widely accessible as possible. The authors' goal is to share the "analytic and aesthetic appeal" of their subject, and on the whole they succeed.The authors state, "This book is, in part, a rendering of the Fisher- Efron-Amari theory and the Jeffreys-Rao Riemannian geometry based on Fisher information. But it is also intended as an introduction to curved exponential families and to subsequent work on several related topics." To make the work more approachable for novices, the book is divided into three sections of increasing difficulty. Part I considers curved exponential families with a one-dimensional parameter; Part II covers multivariate generalizations. Both of these parts are designed to minimize the use of formal differential geometry tools, which are themselves not used extensively until Part III which explores information metric Riemannian geometry. A 30-page appendix on the basic notions of differential geometry accompanies the latter.
Rarely can a statistical subject be studied for its aesthetic appeal, but this is a happy exception. This beauty arises when the results of the tedious Taylor series expansions found in the second-order asymptotic analysis can be "explained" in terms of a few geometric quantities. These quantities describe properties of the models that are independent of the choice of parameterization and so are invariant in the same manner that the curvature of a circle is independent of any method of describing the points on it with a parametric function. In other words, this is a book for a person looking to understand the "big picture" of asymptotic theory. ...
- Wiley Online Library
My reflections, October, 2020:
This book, frankly, has surprised me, in that my appreciation of it has increased with time. A book can present results that are either not strictly novel or, if they are novel, are too minor to be published in articles, yet, according to the book, they have value. Now, nearly 25 years after we finished it, I feel developing the book’s perspective, and digging out for display the many nuggets it contains, was worth the substantial production time and effort.Geometrical Foundations of Asymptotic Inference understands statistical models, fundamentally, as collections of probability distributions that are subject to analysis, meaning calculus, and to cast parameters in the subordinate role of coordinate systems, that is, mappings that allow us to apply calculus.1
The book therefore begins by modifying Efron’s definition of curved exponential families so that they can be characterized, at least locally, by setting to zero some components of a parameter vector. This familiar way we get subfamilies turns out to be equivalent to saying that they can be reparameterized (at least locally) by smooth functions having nonzero derivatives. Thus, for example, we can perform loglikelihood expansions for every well-defined parameterization. The reason for studying curved exponential families is that, even though they, themselves, may not be exponential families (technically, full exponential families) they automatically satisfy the usual regularity conditions needed for asymptotic analysis.2
When I was finishing my 1989 review paper in Statistical Science I was immersed in Bayesian asymptotics (via Laplace’s method). Geometrical Foundations of Asymptotic Inference therefore includes a relatively simple, yet rigorous treatment of posterior expansions. The 1989 paper, and the book, provided, in addition, Bayesian analogues to data-analytic curvature measures that had appeared in the literature, and the Bayesian versions can be computed easily and efficiently using Laplace’s method.
I worked on geometrical methods during my final six months of graduate school, which was enough time to get the results and write the thesis, and I continued along that path as best I could for a few years. But my interest was already waning. Furthermore, I had come across results I wanted, one in particular, that I couldn’t obtain. The decision to invite Paul Vos to help me finish the book was one of the wisest of my career—partly because it taught me to find collaborative assistance whenever I needed it. When the book finally got published, my overwhelming feeling was relief, and, partly because the topic was so specialized, and I had by then published a bunch of papers that aimed to address more immediate issues, I had lingering doubts about its value. From my current vantage point, however, I feel considerable pride, as well as continuing gratitude to Paul.
1. Halmos and Savage (1949, Ann. Math. Statist.) provided a coordinate-free view of sufficiency; I read it during my second semester in graduate school, and it left a lasting impression.
2. Theorem 4.4.2 shows that a curved exponential family, situated within an exponential family with natural parameter space N, is itself an exponential family if and only if it corresponds to an affine subspace of N. For example, a logistic regression model (with an m-dimensional parameter) is itself an exponential family (of dimension m) if and only if the model is linear in the canonical link.
My Philosophy of Statistics
My philosophy of statistics is more-or-less summarized in several pieces:
Kass, R. E. (2021) The Two Cultures: Statistics and Machine Learning in Science, Observational Studies, 7: 135--144.
Kass, R.E. (2011) Statistical Inference: The Big Picture. Statistical Science, 26, 1--20.
Kass, R.E. (2010) How should indirect evidence be used? (Comment on article by Efron) Statistical Science, 25: 166-169.
Kass, R.E. (2006) Kinds of Bayesians (Comment on articles by Berger and by Goldstein), Bayesian Analysis, 1: 437-440.
Kass, R.E. (1998) Comment on "R.A. Fisher in the 21st Century," by Bradley Efron, Statistical Science, 13: 95-122
Also, why is it that Bayes' rule has not only captured the attention of so many people but inspired a religious devotion and contentiousness, repeatedly across many years? Here is my answer.