%  Script runs 1,000 simulations drawing a sample of size 100 from a
%  Poisson distribution, and then plots histograms of the estimated
%  means and estimated variances.
% 
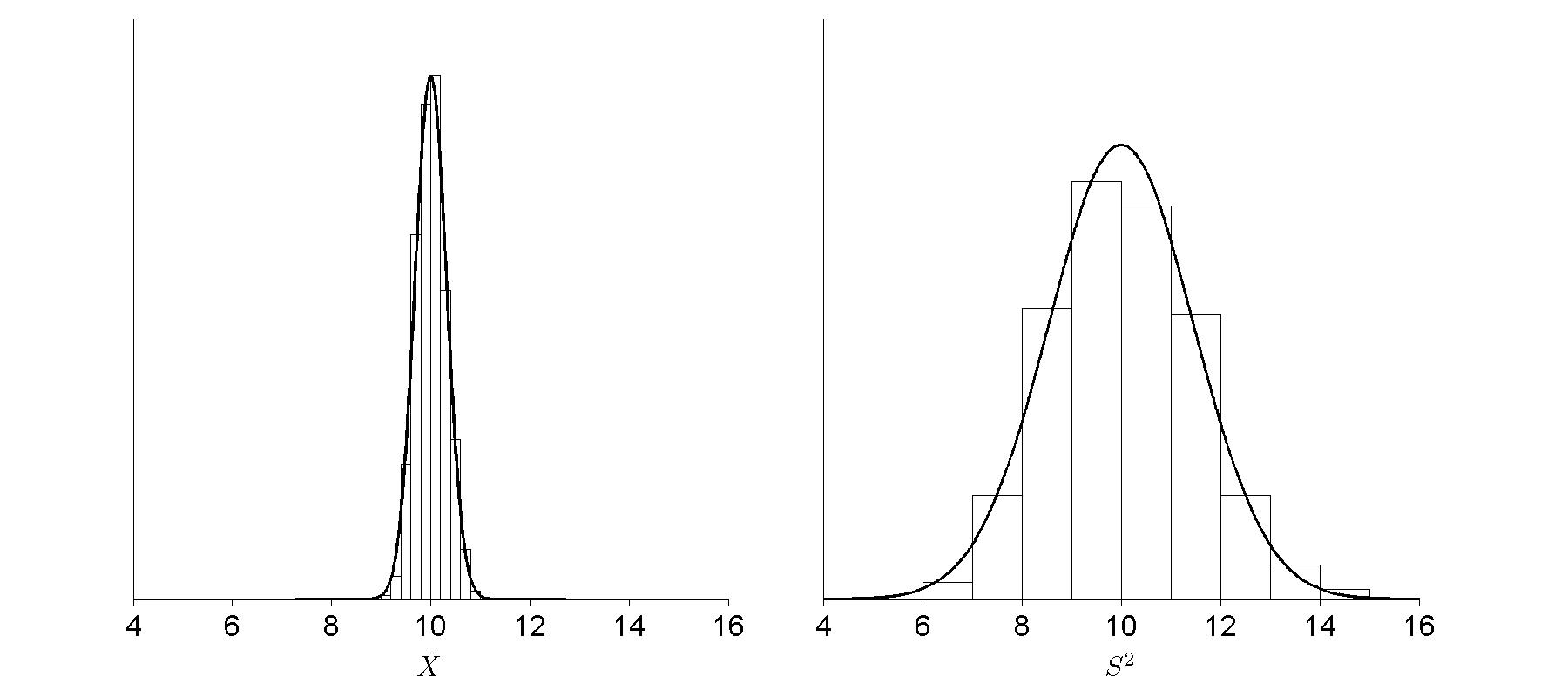
%  Figure caption: Histograms siaplaying distributions of X-bar and S
%  squared based on 1,000 randomly generated samples of size n = 100
%  froma Poisson distribution with mean parameter mu = 10.  In these
%  repeated samples, both X-bat and S squared have distributions that
%  are approximately normal.  Both distributions are centered at 10
%  (both estimators are unbiased) but the values of S squared
%  fluctuate much more than do the values of X-bar.

nSimulations = 1000;
nSamples     = 100;
lambda       = 10;

%  To obtain 1000 samples of size 100, we sample a matrix with 100
%  rows and 1000 columns.  Each column is a simulation.  
psample = poissrnd(10, 100, 1000);

%  mean and var, when the input is a matrix, by default takes the
%  mean (or variance) across a column.  
sampleMeans = mean(psample);
sampleVariances = var(psample);

x_vals = 4:0.01:16;
x_vals1 = 4.1:0.2:15.9;
x_vals2 = 4.5:1:15.5;

%% Histogram of sample means                    %%
subplot(1, 2, 1)
bar(x_vals1, hist(sampleMeans, x_vals1)./trapz(x_vals1, hist(sampleMeans, x_vals1)), 'style', 'hist')
set(gca, 'Box', 'off', 'FontSize', 20, ...
         'XLim', [4, 16], ...
         'XTick', 4:2:16, 'YTick', [], 'TickDir', 'out')

%  Set faces to be white.  
meanhist = findobj(gca, 'Type', 'patch');
set(meanhist, 'FaceColor', 'w')

y_vals1 = normpdf(x_vals, lambda, sqrt(lambda/nSamples));
hold on;
plot(x_vals, y_vals1, '-k', 'LineWidth', 2)

xlabel({''; '$\bar{X}$'}, 'Interpreter', 'LaTex', 'FontSize', 20)

%  Position the device.  
set(gcf, 'Position', [100, 100, 1800, 800])
set(gca,'OuterPosition',get(gca,'OuterPosition')+[-0.05, 0.025, 0.05, 0.025])

%%  Histogram of sample variances               %%
subplot(1, 2, 2)
bar(x_vals2, hist(sampleVariances, x_vals2)./trapz(x_vals2, hist(sampleVariances, x_vals2)), 'style', 'hist')
set(gca, 'Box', 'off', 'FontSize', 20, ...
         'XLim', [4, 16], ...
         'XTick', 4:2:16, 'YTick', [], 'TickDir', 'out')

%  Set faces to be white. 
varhist = findobj(gca, 'Type', 'patch');
set(varhist, 'FaceColor', 'w')

y_vals2 = normpdf(x_vals, lambda, sqrt((lambda/nSamples)+2*(lambda^2/(nSamples-1))));
hold on;
plot(x_vals, y_vals2, '-k', 'LineWidth', 2)

xlabel({''; '$S^2$'}, 'Interpreter', 'LaTex', 'FontSize', 20)

set(gca,'OuterPosition',get(gca,'OuterPosition')+[-0.05, 0.025, 0.05, 0.025])