Out of sample predictive
validation
The following table gives percent change in
MSE for the
hold-out sample compared with the predictions of the individual LS
models.
I'll split the data set into two parts -- take the first half and the
second half and do an equal split. I estimate the model on the
first half and then, based on the prior, I ask how well
I can predict in each of these outer sample data sets. So in the
first case, if I do the individual least-square
model, I'm going to measure everything relative to that and
think about what's the average mean square area. The
following table gives percentage change in MSE for the hold-out sample
compared with the predictions of the individual LS models.
A pool model would bring it down by
10%, a pool and a cluster model create similar, the cluster does
it a little better, but not much. Now, if I do a Bayes approach
with a v prior, (if I said k=5) I've essentially said that
there's not a lot of differences in my prior between this and
the initial least-square estimates. So it makes sense that these
things are close.
If I start saying that my Bayes k
parameter is moderate (for instance if I say that k=1)
I start coming up with a 17% decrease in auto sample least-squared.
On the other hand, if I finally go to a strong Bayes prior,
say it's equal to .1, 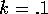 , what
happens is a big
decrease in least-squared error -- approximately a 25% decrease. The
point isn't to try to chose my k to
minimize the outer sample mean-squared area. All I'm trying to
do is take into account that my prior notions before going into this
are that the demographics are important. If I had to
do this I would say I'd like to go to a pool model, but I know
a pool model is wrong, so what the data is essentially telling
me is that there is some support for either this moderate or this
strong prior. The problem is that the data isn't really formally
telling me which one should I go to. It's almost saying more is
better, but it's going to be difficult to discriminate. For more detail
see here. Yes?
, what
happens is a big
decrease in least-squared error -- approximately a 25% decrease. The
point isn't to try to chose my k to
minimize the outer sample mean-squared area. All I'm trying to
do is take into account that my prior notions before going into this
are that the demographics are important. If I had to
do this I would say I'd like to go to a pool model, but I know
a pool model is wrong, so what the data is essentially telling
me is that there is some support for either this moderate or this
strong prior. The problem is that the data isn't really formally
telling me which one should I go to. It's almost saying more is
better, but it's going to be difficult to discriminate. For more detail
see here. Yes?
Question from Robert E. Kass:
Question from Robert McCulloch:
Question from Robert E. Kass:
 Previous Section
Previous Section
 Next Section
Next Section
 Go to Table of Contents
Go to Table of Contents
 Go to written version of paper
Go to written version of paper
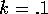 , what
happens is a big
decrease in least-squared error -- approximately a 25% decrease. The
point isn't to try to chose my k to
minimize the outer sample mean-squared area. All I'm trying to
do is take into account that my prior notions before going into this
are that the demographics are important. If I had to
do this I would say I'd like to go to a pool model, but I know
a pool model is wrong, so what the data is essentially telling
me is that there is some support for either this moderate or this
strong prior. The problem is that the data isn't really formally
telling me which one should I go to. It's almost saying more is
better, but it's going to be difficult to discriminate. For more detail
see here. Yes?
, what
happens is a big
decrease in least-squared error -- approximately a 25% decrease. The
point isn't to try to chose my k to
minimize the outer sample mean-squared area. All I'm trying to
do is take into account that my prior notions before going into this
are that the demographics are important. If I had to
do this I would say I'd like to go to a pool model, but I know
a pool model is wrong, so what the data is essentially telling
me is that there is some support for either this moderate or this
strong prior. The problem is that the data isn't really formally
telling me which one should I go to. It's almost saying more is
better, but it's going to be difficult to discriminate. For more detail
see here. Yes?
 Previous Section
Previous Section