What I was saying was that I
don't need to really say anything about the error covariance
matrices so I'm going to have a diffuse prior. This will
be non-informative. On top of that I don't really want to
say anything about the demographics, so again, I'll have
a diffuse prior of that. Now, what is going to be important is
to say something about this random variation across the stores.
You remember that I've got 192 parameters.
The problem I'm running into is that I only
have 83 stores, so if I don't have an informative prior, then I'm
not going to have a well-defined Wishart distribution. For
the Wishart to be defined, I've got to have an informative prior
at this stage. This causes some problems because I
don't exactly know what this prior should be.
There's going to be all these scaling differences
such as what is the price elasticity for Minute Maid, and does that vary
more than the price elasticity for Tropicana. So what I'm going
to do is do a
kind of empirical technique to try to set the prior on this
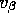 .
I'm going to essentially
postulate that there is some type of independent relationships
for this prior on each of these parameters and
I'm going to compute the least squares estimates. Then
I'm going to take the variance of those and
scale those by k. I also want to include the
.
I'm going to essentially
postulate that there is some type of independent relationships
for this prior on each of these parameters and
I'm going to compute the least squares estimates. Then
I'm going to take the variance of those and
scale those by k. I also want to include the 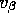 in there, and it's easier just to think about this
in terms of what are the expectations of my prior. Well, the
expectation of my prior is down here, so the expectation is
essentially going to be this matrix here: this
in there, and it's easier just to think about this
in terms of what are the expectations of my prior. Well, the
expectation of my prior is down here, so the expectation is
essentially going to be this matrix here: this 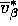 .
So I've got the k's and the k's are sort of
telling me what's the expectation. k is 1 and that my
expectation would be
.
So I've got the k's and the k's are sort of
telling me what's the expectation. k is 1 and that my
expectation would be 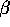 is essentially going back - it's
putting me at the same place that I would start from an empirical prior.
is essentially going back - it's
putting me at the same place that I would start from an empirical prior.
For more detail on specification of the prior click
here. Also, see here.
For the outline click here.
The reason I chose this parameterization is that I'd like
to have something that puts me somewhere close to
the least-squared estimates, somewhere that's close to the pooled
estimates, and somewhere between the pooled and the least squares estimates.
If my k=0 and my 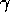 is 0, then my prior is going to
say that there's no demographic effects -- it's essentially going
to mimic a pool model.
There's no cross-store variation and there's no demographic effects
so what we want to
think about is this: I've got my individual parameter of
is 0, then my prior is going to
say that there's no demographic effects -- it's essentially going
to mimic a pool model.
There's no cross-store variation and there's no demographic effects
so what we want to
think about is this: I've got my individual parameter of
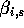 and that's going to equal
this
and that's going to equal
this 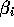 and
this
and
this 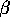 plus the demographic
effects, plus this independent
variable or this random variable. The next case is going to
say that we've got some type of direct demographic independent
interactions. The
next question is where should I set the k? Should k be small,
should k be large? If I set k large, then the
estimates are going to converge to the individual store models,
It's essentially like saying that
each of the stores is unrelated to all the others. The other
option is to just set k=1, so it's essentially
a type of empirical Bayes prior. An additional option is to
set k to a small value: suppose I said
plus the demographic
effects, plus this independent
variable or this random variable. The next case is going to
say that we've got some type of direct demographic independent
interactions. The
next question is where should I set the k? Should k be small,
should k be large? If I set k large, then the
estimates are going to converge to the individual store models,
It's essentially like saying that
each of the stores is unrelated to all the others. The other
option is to just set k=1, so it's essentially
a type of empirical Bayes prior. An additional option is to
set k to a small value: suppose I said 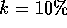 of the
empirical Bayes prior. How do I determine what would be a
good k? Well, if I was following a pure approach I would
just say k
is this number, or if I wasn't sure about it, I would pick some
kind of prior on the k. Now in this case, I'm interested in
what this k should be, so I'm going
to go back and allow the k to vary.
of the
empirical Bayes prior. How do I determine what would be a
good k? Well, if I was following a pure approach I would
just say k
is this number, or if I wasn't sure about it, I would pick some
kind of prior on the k. Now in this case, I'm interested in
what this k should be, so I'm going
to go back and allow the k to vary.
How we choose our final hyperparameter is given
here.
 Previous Section
Previous Section
 Next Section
Next Section
 Go to Table of Contents
Go to Table of Contents
 Go to written version of paper
Go to written version of paper
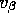 .
I'm going to essentially
postulate that there is some type of independent relationships
for this prior on each of these parameters and
I'm going to compute the least squares estimates. Then
I'm going to take the variance of those and
scale those by k. I also want to include the
.
I'm going to essentially
postulate that there is some type of independent relationships
for this prior on each of these parameters and
I'm going to compute the least squares estimates. Then
I'm going to take the variance of those and
scale those by k. I also want to include the 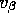 in there, and it's easier just to think about this
in terms of what are the expectations of my prior. Well, the
expectation of my prior is down here, so the expectation is
essentially going to be this matrix here: this
in there, and it's easier just to think about this
in terms of what are the expectations of my prior. Well, the
expectation of my prior is down here, so the expectation is
essentially going to be this matrix here: this 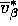 .
So I've got the k's and the k's are sort of
telling me what's the expectation. k is 1 and that my
expectation would be
.
So I've got the k's and the k's are sort of
telling me what's the expectation. k is 1 and that my
expectation would be 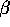 is essentially going back - it's
putting me at the same place that I would start from an empirical prior.
is essentially going back - it's
putting me at the same place that I would start from an empirical prior.
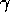 is 0, then my prior is going to
say that there's no demographic effects -- it's essentially going
to mimic a pool model.
There's no cross-store variation and there's no demographic effects
so what we want to
think about is this: I've got my individual parameter of
is 0, then my prior is going to
say that there's no demographic effects -- it's essentially going
to mimic a pool model.
There's no cross-store variation and there's no demographic effects
so what we want to
think about is this: I've got my individual parameter of
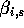 and that's going to equal
this
and that's going to equal
this 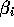 and
this
and
this 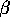 plus the demographic
effects, plus this independent
variable or this random variable. The next case is going to
say that we've got some type of direct demographic independent
interactions. The
next question is where should I set the k? Should k be small,
should k be large? If I set k large, then the
estimates are going to converge to the individual store models,
It's essentially like saying that
each of the stores is unrelated to all the others. The other
option is to just set k=1, so it's essentially
a type of empirical Bayes prior. An additional option is to
set k to a small value: suppose I said
plus the demographic
effects, plus this independent
variable or this random variable. The next case is going to
say that we've got some type of direct demographic independent
interactions. The
next question is where should I set the k? Should k be small,
should k be large? If I set k large, then the
estimates are going to converge to the individual store models,
It's essentially like saying that
each of the stores is unrelated to all the others. The other
option is to just set k=1, so it's essentially
a type of empirical Bayes prior. An additional option is to
set k to a small value: suppose I said 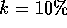 of the
empirical Bayes prior. How do I determine what would be a
good k? Well, if I was following a pure approach I would
just say k
is this number, or if I wasn't sure about it, I would pick some
kind of prior on the k. Now in this case, I'm interested in
what this k should be, so I'm going
to go back and allow the k to vary.
of the
empirical Bayes prior. How do I determine what would be a
good k? Well, if I was following a pure approach I would
just say k
is this number, or if I wasn't sure about it, I would pick some
kind of prior on the k. Now in this case, I'm interested in
what this k should be, so I'm going
to go back and allow the k to vary.
 Previous Section
Previous Section