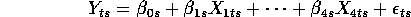
83 Store Multivariate Linear Models
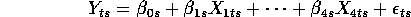
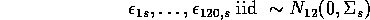
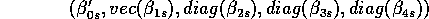

Note!
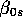 is 12
is 12  1
1
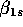 is 12
is 12  12 (price coefficients)
12 (price coefficients)
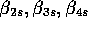 are each diagonal 12
are each diagonal 12  12
12
Compared to Blattberg & George (1991), this is a much more complete model which:
It looks like the same formulation, with four instead of eight variables. But these are multivariate linear models. Here there is one model for each store where I had one model for each brand-chain. Before we had four brands of toilet paper and three chains so there were 12 time series.
There are ways you might think about combining those estimates.
Here within each store he had 12 1 price categories. He
explains movement of a 12-dimensional vector and how it relates to
prices of all variables and characteristics of all of them. Each is
a diagonal 12
1 price categories. He
explains movement of a 12-dimensional vector and how it relates to
prices of all variables and characteristics of all of them. Each is
a diagonal 12 12 matrix. The coefficient,
12 matrix. The coefficient, 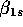 , is
non-diagonal. The top row of
, is
non-diagonal. The top row of 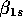 is
is 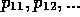 ,
etc. It is a matrix of cross-elasticities. So, if I increase the
price of the first product, this is the coefficient that tells you
how demand will change. It's linear so if I change the price of the
next one this is how much the demand will change. What's built
in here is all of the different changes you will get as the price
varies.
,
etc. It is a matrix of cross-elasticities. So, if I increase the
price of the first product, this is the coefficient that tells you
how demand will change. It's linear so if I change the price of the
next one this is how much the demand will change. What's built
in here is all of the different changes you will get as the price
varies.
This is picking up a lot more information. Whereas we were just
shrinking different 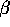 's to themselves, what Alan has done here
is really think about modeling all the different interrelationships
between products.
's to themselves, what Alan has done here
is really think about modeling all the different interrelationships
between products.
Shrinkage is to compensate for variability that you can't explain. It makes much more sense to try to explain the variation. This is a much more comprehensive model. He has the full-blown model: not i.i.d. errors. Geweke said you shouldn't assume when you have multiple equations that the errors will be i.i.d.
Advantages of using a Bayesian approach with such a model:
Once you have a complete stochastic model for the whole setup then you can think about simulation -- in the confines of your data -- of changes. What Alan is able to consider is pricing changes and see the consequences on profits.
I'm doing another application having to do with estimating machine failure rates and we only have partial data. When you put a fully Bayesian model you can actually simulate the unseen failures. So the client is astonished. Data is the boundary of uncertainty and you simulate within that boundary what's going on. It's very powerful: one of the aspects that can take off.
 Go to written version of paper
Go to written version of paper