Some Critical Remarks

a.

Alternative Model: A better straw man than the pooled model is the model

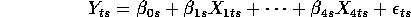
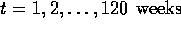
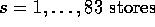
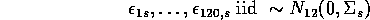
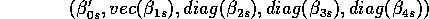
It would be interesting to know how well the previous estimates fare compared to the restricted MLEs for this model

Figure 1 suggests a good fit.

Let me put up the diagram that you saw. These open boxes are the least-squares estimates and the black ones are the Bayes estimates. The pooled ones run straight across. I was also confused with Andrew's question and asked Alan yesterday.

This is the mean of the 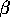's in the model. This equals 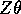. What's happening is that if I do the Bayes model I am shrinking everything towards this mean function, which is a function of demographics. The pooled estimate ignores demographics and just collapses everything together.

It seems to me, one tries to estimate what's Bayes and what's not Bayes. I think someone else was making this point as well. It would be interesting to compare that model with one which simply restricts the 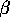's to be right on that line. You could use restricted maximum likelihood to estimate that. In one way this is how well you've done with the model and in comparison with Bayes shows how well you've freed things up using the Bayesian model. What's nice with Bayes is once you're through with REML, what then? You don't have the luxury of simulation and other aspects.

b.

Hyperparameters: Because selection of hyperparameters is difficult, the consequences of various settings are explored. For instance, different values of K to see what will happen.

• Advantage

  Provides evidence of robustness. It is comforting. Things are not that sensitive. Boxplots don't change much for ``store sensitivities''.

• Disadvantage

  Yields an added dimension of uncertainty which is not conveyed by the posterior. Put another way, which posterior should we believe? You should put a simple prior on K to give you some sense of variation.

It is curious that the posterior based on the weakest prior offers the most potential for profit improvement (see table 6). For the strong prior, depending on the scenario, it leads up to 25% improvement. But if you use the weak prior you can actually do much better. Careful, by not constraining LS-estimates, the sky is the limit. More variation yields more pretending. This leads to the problem: prior-utility confusion. What's really going on?

Dilemma: Should prior selection be based on such utility considerations even if it defeats the uncertainty interpretation of the posterior?

c.

Predictive Cross-Validation:

Selection of hyperparameters by predictive cross-validation (PCV) will lead to overshrinkage. Cutting data in half; using one half to select for the other. Intuitively, if you throw away part of your data you have less precise estimation. If you have less precise estimation, you will want to shrink more. The next example illustrates this.

A Simple Example:

Suppose

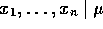iid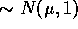

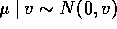
Then

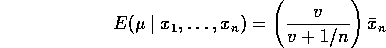
so that

is the ``correct'' amount of shrinkage.

However, estimation of 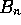by PCV will tend to make it too large. Why?

By the law of large numbers,

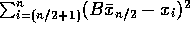
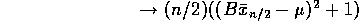
so that 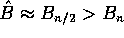, an overestimate!

You could probably work out how you should correct for this problem. So, the diagrams where you show that if I change K I get this much improvement could be a little misleading.

Previous Section

Next Section

Go to Table of Contents

Go to written version of paper