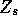for 
?
For 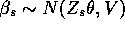such hierarchical models to be effective, a crucial modeling issue is
How to select 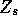for ?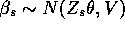
I.e., what prior mean for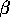 
should we be thinking in these
large models? In Blattberg and George we just used linear constraints
to project into simple subspaces for each cluster. What Alan has
done is add demographic variables
here. You have a different type
of shrinkage. It is interesting--one might think at first, put
demographic variables right into the demand equations. It's much
smarter to think of it as an aggregate effect and so put it in for
the 
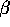's.
You don't get handed the data set that you see on the Web. What you get is some horrible messy data, start cleaning it, decide what variables you want, and how you want to measure those variables. You have to build all of this modeling. When you give people data you give them your cleaned up data--the data that goes with your model.
How do you go about building or selecting the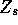 
? Rob and I have started this.
A step in this direction: Model Building Methods for Exchangeable Regressions (George & McCulloch 1994).
Setup: Observe Y and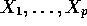 
across M subpopulations
Goal: To build a hierarchical model
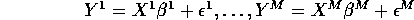
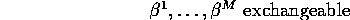
The Variable Selection Problem: To select a subset from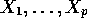 
to include across all M regressions.
In Blattberg and George what I did was build one regression at a time. Everything needs to be symmetric. So, suppose a variable goes in two of the models but not in ten of the others? How do you make that decision? Formalize the problem. Another problem is the coefficient restriction problem: using the same coefficient for X across all M regressions. This is a subspace problem. In fact, what Ross was doing was exactly this. It's trying to make decisions simultaneously about a lot of different coefficients across a hierarchical model.
Our approach: Model relevant uncertainty with a hierarchical mixture:
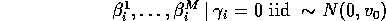
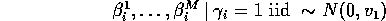
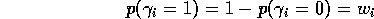
Hyperparameter calibration:
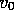small so that
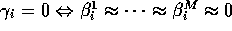
large so that
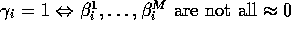
Relevant model building information can now be obtained from
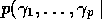data)
This last slide is the same diagram seen yesterday. Now what we
are saying is that all of the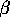 
's across all of the models
come from this concentrated versus diffuse distribution. And now
look at various changes in this. If I center everything at 0, I am
thinking about variable selection. If I center everything about an
arbitrary constant, I am thinking about setting everything equal.
This is another direction and something that needs to be addressed.
At first, what Alan has done is put down model specification, but
realistically what we all do is use data to come up with model
specification. This needs to be formalized and can lead to good
methods.
Go to written version of paper