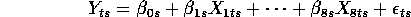
12 Chain-Brand Univariate Linear Models
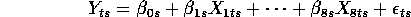
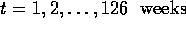
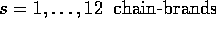
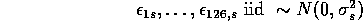
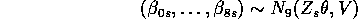
Paper compares various empirical Bayes and fully Bayes estimates and predictions.
Here's the Blattberg and George model. For me this is a simple
situation and you can see how Alan elaborated on this to get a more
comprehensive and meaningful model. We had a baby problem: 12
separate univariate linear models or time series, 126 weeks of data
for each of these. The response was log demand. The variables
were, for example,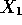 
for price. So if you increase the price,
the coefficient 
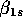was negative or you expect it to be
negative meaning that the quantity you sold went down.
Blattberg said these models are crazy. You get signs all over the place. The idea is to get approved estimates. How to do this? It is natural to think of it in the context of a hierarchical model. We found after testing and model building that it is safe to assume some i.i.d. structure here.
For the second structure, the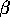 
's draw from a Normal
distribution. The basic idea was projecting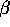 
into different
subspaces. We only considered simple cases--for instance, different
groupings of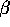 
-vectors. One
simple example was 
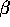-vectors
for each of the 12 models as i.i.d. Estimates and predictions were
compared for various empirical Bayes and fully Bayes methods. Things
had the right sign so seemed better.
But I wondered, could this stuff really be used realistically for setting pricing promotional strategies? What you need to do is go much further. That's what Alan has done.
Go to written version of paper