Before I go into the specification of the prior, I want to ask,
suppose I know what all the priors were and
I've got all the data, how do I estimate this model?
I've got everything in a natural conjugate form, so you might
think that it's fairly easy, but the problem is that these
Wishart distributions are going to cause some problems here.
If I knew what the 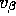 was
beforehand and if I knew the
error covariance matrices, I could skip a lot of this and
just say that I know exactly from normal theory and
hierarchical Bayesian models how to solve this
problem, but we need to integrate out these Wishart
distributions. To try to compute the marginal
distribution of this
was
beforehand and if I knew the
error covariance matrices, I could skip a lot of this and
just say that I know exactly from normal theory and
hierarchical Bayesian models how to solve this
problem, but we need to integrate out these Wishart
distributions. To try to compute the marginal
distribution of this 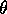 is going to be very difficult, so
we've got to come up with some alternative estimators. As I
mentioned, one thing you might want to use is to assume
we knew what the
is going to be very difficult, so
we've got to come up with some alternative estimators. As I
mentioned, one thing you might want to use is to assume
we knew what the 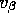 was. Let's come up with some kind of
empirical estimator and then just substitute that and treat it
as null. Another thing you might want to do is some kind of
two-stage estimation -- estimate all
the stores separately and then in a second stage go back
and regress these on the demographics. You might want to go
further than that and do some kind of iterated estimator. Finally
what you could do is the Gibbs Sampler. The Gibb's sampler is
going to fit really nicely because with the normal Wishart, you've
got to have all these nicely defined distributions, you're also
going have these natural conjugate priors and it's going to make
the problem pretty easy to follow through.
was. Let's come up with some kind of
empirical estimator and then just substitute that and treat it
as null. Another thing you might want to do is some kind of
two-stage estimation -- estimate all
the stores separately and then in a second stage go back
and regress these on the demographics. You might want to go
further than that and do some kind of iterated estimator. Finally
what you could do is the Gibbs Sampler. The Gibb's sampler is
going to fit really nicely because with the normal Wishart, you've
got to have all these nicely defined distributions, you're also
going have these natural conjugate priors and it's going to make
the problem pretty easy to follow through.
 Previous Section
Previous Section
 Next Section
Next Section
 Go to Table of Contents
Go to Table of Contents
 Go to written version of paper
Go to written version of paper
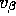 was
beforehand and if I knew the
error covariance matrices, I could skip a lot of this and
just say that I know exactly from normal theory and
hierarchical Bayesian models how to solve this
problem, but we need to integrate out these Wishart
distributions. To try to compute the marginal
distribution of this
was
beforehand and if I knew the
error covariance matrices, I could skip a lot of this and
just say that I know exactly from normal theory and
hierarchical Bayesian models how to solve this
problem, but we need to integrate out these Wishart
distributions. To try to compute the marginal
distribution of this 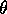 is going to be very difficult, so
we've got to come up with some alternative estimators. As I
mentioned, one thing you might want to use is to assume
we knew what the
is going to be very difficult, so
we've got to come up with some alternative estimators. As I
mentioned, one thing you might want to use is to assume
we knew what the 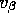 was. Let's come up with some kind of
empirical estimator and then just substitute that and treat it
as null. Another thing you might want to do is some kind of
two-stage estimation -- estimate all
the stores separately and then in a second stage go back
and regress these on the demographics. You might want to go
further than that and do some kind of iterated estimator. Finally
what you could do is the Gibbs Sampler. The Gibb's sampler is
going to fit really nicely because with the normal Wishart, you've
got to have all these nicely defined distributions, you're also
going have these natural conjugate priors and it's going to make
the problem pretty easy to follow through.
was. Let's come up with some kind of
empirical estimator and then just substitute that and treat it
as null. Another thing you might want to do is some kind of
two-stage estimation -- estimate all
the stores separately and then in a second stage go back
and regress these on the demographics. You might want to go
further than that and do some kind of iterated estimator. Finally
what you could do is the Gibbs Sampler. The Gibb's sampler is
going to fit really nicely because with the normal Wishart, you've
got to have all these nicely defined distributions, you're also
going have these natural conjugate priors and it's going to make
the problem pretty easy to follow through.
 Previous Section
Previous Section