 , ...,
, ..., 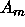 ,
then the argument above extends to show that
,
then the argument above extends to show that
If we are contemplating making m inferences  , ...,
, ..., 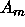 ,
then the argument above extends to show that
,
then the argument above extends to show that
The way to adjust inferences for multiple comparisons is to consider
all of the inferences one is likely to make, and then use equation
(2)---or exploit the structure of the regression/ANOVA model to
get around (2)---to compute what the confidence level for each
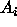 should be so that
should be so that 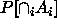 is at least
is at least 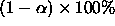 .
.
For linear models in general, and ANOVA models in particular, there are three common ways of doing this:
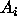 's are whatever
particular CI's that you are interested in. It is easy to see, by
induction from (2) for two events, that
's are whatever
particular CI's that you are interested in. It is easy to see, by
induction from (2) for two events, that
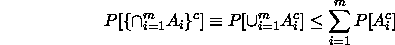
and so
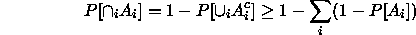
This suggests that if we want 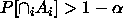 , we should take
, we should take
 .
.
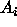 's are CI's for all
possible contrasts
's are CI's for all
possible contrasts 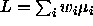 with
with 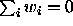 . The
essential idea is that for the contrast L, (1) tells us
that a confidence interval will be of the form
. The
essential idea is that for the contrast L, (1) tells us
that a confidence interval will be of the form

For a single CI, we would use the upper 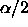 tail cutoff for a
tail cutoff for a
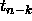 distribution,
distribution,
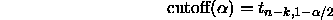
Scheffé's remarkable result is that if you replace this with the
square root of a scaled upper-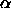 tail cutoff for an F
distribution,
tail cutoff for an F
distribution,
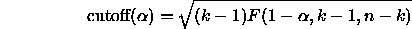
all resulting intervals for every possible contrast L
will have confidence 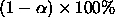 .
.
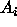 's
are CI's for all pairwise comparisons
's
are CI's for all pairwise comparisons  . The idea is
essentially the same as Scheffé, except that
. The idea is
essentially the same as Scheffé, except that
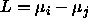 ; and
; and
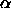 tail cutoff of the
``studentized range'' distribution q,
tail cutoff of the
``studentized range'' distribution q,
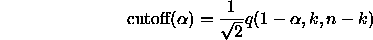
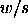 where w
is the range
where w
is the range 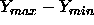 of a random sample of size k from
of a random sample of size k from
 , and
, and 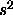 is a n-k degrees of freedom estimate of
is a n-k degrees of freedom estimate of
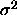 , independent of w).
, independent of w).
Naturally one wants to choose the method that leads to the narrowest intervals, but also has a defensible confidence statement. The following guidlines more or less follow Neter, Wasserman and Kutner (1990, p. 589).
 ,
Tukey's method is better (leads to narrower intervals) than
Bonferroni.
,
Tukey's method is better (leads to narrower intervals) than
Bonferroni.
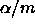 .
.
In SPLUS there is a special function multicomp() that handles the details of multiple comparisons. Here are some examples of its use with the coag dataset.
402 > coag.mca _ multicomp(coag.aov,focus="diet")
402 > coag.mca
95 % simultaneous confidence intervals for specified
linear combinations, by the Tukey method
critical point: 2.7987
response variable: coag
intervals excluding 0 are flagged by '****'
Estimate Std.Error Lower Bound Upper Bound
A-B -4.710 1.50 -8.90 -0.515 ****
A-C -4.380 1.50 -8.57 -0.181 ****
A-D 2.370 1.70 -2.38 7.130
B-C 0.333 1.60 -4.15 4.820
B-D 7.080 1.79 2.07 12.100 ****
C-D 6.750 1.79 1.74 11.800 ****
402 > plot(coag.mca)
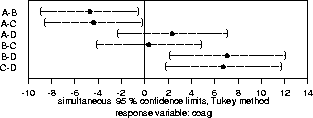
The multicomp() procedure does exactly what is indicated in item #5 above: it tries several methods (including the three mentioned above) of doing multiple comparisons, and then reports to us the best (narrowest intervals) method. You can force it to try a few more computer-intensive methods by saying method="best", or you can force it to use a particular method by specifying the method. Some method choices include:
402 > multicomp(coag.aov,focus="diet",comparisons="none", + method="lsd",error.type="cwe",plot=T) 95 % non-simultaneous confidence intervals for specified linear combinations, by the Fisher LSD method critical point: 2.086 response variable: coag intervals excluding 0 are flagged by '****' Estimate Std.Error Lower Bound Upper Bound A 62.1 0.981 60.1 64.2 **** B 66.8 1.130 64.5 69.2 **** C 66.5 1.130 64.1 68.9 **** D 59.8 1.390 56.9 62.6 ****
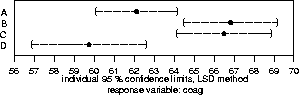
Similarly, you could get multicomp() to give the ``uncorrected'' confidence intervals we calculated above when contrasts were introduced, by dropping the ``comparisons="none"'' parameter.
402 > multicomp(coag.aov,focus="diet",method="lsd",error.type="cwe",plot=T)
method="lsd" stands for Fisher's method of least significant differences, which is precisely the unadjusted t intervals we first calculated. Since it has R. A. Fisher's name attached to it, lots of nonstatisticians use it (try searching for `` +Fisher +"least significant difference"'' in Alta-Vista!); however this method does not protect against the degradation of confidence levels in multiple CI's, and it is not much better than the 68%-95%-99% eyeball rule from Statistics 36-201.