Grand Mean plus Effects model

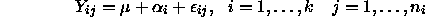
Last time we also talked about the ``grand mean plus effects'' parameterization,

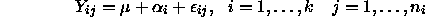
The relationship of this model to the cell means model

is that 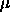is supposed to be an average of the 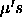, and that .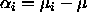

The grand mean plus effects model has k+1 parameters, 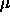, , 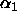..., 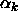and only k cell means to estimate, so some sort of linear constraint is needed to make the model work. There are several different ways to impose a ``sum to zero'' constraint, each corresponding to a different ``grand mean'':

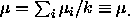• Unweighted Mean. If we take , it follows that

  

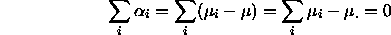
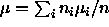• Sample Size Weighted Mean. If we take , then it follows that

  

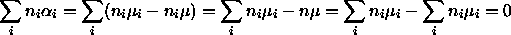
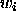• A-priori Weighted Mean. If there are some external weights such that 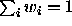and we define , it similarly follows that

  

is an unbiased estimator of the grand mean 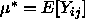. It can be shown that if 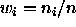(sample size weights) this estimator has the least possible variance (this is a nice exercise in multivariate differential calculus).

It's easy to see that the model.tables() function gives you the sample-size weighted effects when you specify type="effects":

402 > model.tables(coag.aov,type="effects")
Refitting model to allow projection
Tables of effects

 diet 
         A     B   C     D 
    -1.875 2.833 2.5 -4.25
rep  8.000 6.000 6.0  4.00
402 > sum(scan())
1:   -1.875 2.833 2.5 -4.25
5: 
[1] -0.792
402 > sum(scan()*scan())
1:   -1.875 2.833 2.5 -4.25
5: 
1:  8.000 6.000 6.0  4.00
5: 
[1] -0.002

One can fit the unweighted effects model directly by telling SPLUS what kind of contrasts to use:

402 > coag.sum.aov _ aov(coag ~ diet,data=coag,contrasts=list(diet=contr.sum))
402 > coefficients(coag.sum.aov)
 (Intercept)     diet1   diet2    diet3 
    63.80208 -1.677083 3.03125 2.697917
402 > co _ .Last.value
402 > c(co[2:4],-sum(co[2:4]))
     diet1   diet2    diet3           
 -1.677083 3.03125 2.697917 -4.052083
402 > co[1] + c(co[2:4],-sum(co[2:4]))
  diet1    diet2 diet3       
 62.125 66.83333  66.5 59.75
402 > model.tables(coag.aov,type="means")$tables$diet
Refitting model to allow projection
      A        B    C     D 
 62.125 66.83333 66.5 59.75

402 > summary.lm(coag.sum.aov)

Call: aov(formula = coag ~ diet, data = coag, contrasts = list(diet = contr.sum))
Residuals:
    Min     1Q Median    3Q Max 
 -3.833 -2.583  0.375 1.312 4.5

Coefficients:
                Value Std. Error   t value  Pr(>|t|) 
(Intercept)   63.8021    0.5838   109.2923    0.0000
      diet1   -1.6771    0.9066    -1.8499    0.0792
      diet2    3.0313    0.9911     3.0585    0.0062
      diet3    2.6979    0.9911     2.7221    0.0131

Residual standard error: 2.775 on 20 degrees of freedom
Multiple R-Squared: 0.5472 
F-statistic: 8.056 on 3 and 20 degrees of freedom, the p-value is 0.001028 

Correlation of Coefficients:
      (Intercept)   diet1   diet2 
diet1 -0.1894                    
diet2 -0.0346     -0.2454        
diet3 -0.0346     -0.2454 -0.3061
402 > # 
402 > # now use the information in the summary to construct a
402 > # point estimate and se for the effect of the fourth diet ("D")
402 > #
402 > diet4 _ c(0,-1,-1,-1)
402 > diet4 %*% coefficients(coag.sum.aov)
          [,1] 
[1,] -4.052083
402 > diet4 %*% summary.lm(coag.sum.aov)$cov.unscaled %*% diet4
          [,1] 
[1,] 0.1692708
402 > sqrt(.Last.value)
          [,1] 
[1,] 0.4114254

One can do something similar with the cell means model:

402 > coag.tx.aov _ aov(coag ~ diet,data=coag,contrasts=list(diet=contr.treatment))
402 > summary.lm(coag.tx.aov)

Call: aov(formula = coag ~ diet, data = coag, contrasts = list(diet = contr.treatmen
t))
Residuals:
    Min     1Q Median    3Q Max 
 -3.833 -2.583  0.375 1.313 4.5

Coefficients:
               Value Std. Error  t value Pr(>|t|) 
(Intercept)  62.1250   0.9809    63.3322   0.0000
      dietB   4.7083   1.4984     3.1422   0.0051
      dietC   4.3750   1.4984     2.9198   0.0085
      dietD  -2.3750   1.6990    -1.3979   0.1775

Residual standard error: 2.775 on 20 degrees of freedom
Multiple R-Squared: 0.5472 
F-statistic: 8.056 on 3 and 20 degrees of freedom, the p-value is 0.001028 

Correlation of Coefficients:
      (Intercept)   dietB   dietC 
dietB -0.6547                    
dietC -0.6547      0.4286        
dietD -0.5774      0.3780  0.3780

SPLUS has several kinds of built-in ``contrast'' options, that are used to reparametrize an ANOVA model. They are:

• contr.treatment produces coefficients that are are just the differences between level 1 and levels 2 through k of the factor.
• contr.sum produces coefficients satisfying the constraint that their sum is zero (the traditional analysis of variance parametrization).
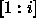• contr.helmert contrasts are equivalent to taking differences between level i+1 and the average of levels , in the unweighted effects model. So for example if 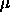is the grand mean and 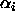are the unweighted effects for level i (so all the 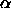's sum to zero), the parameters 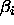for the Helmert contrasts are related to the effects 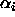in the unweighted effects model by

  

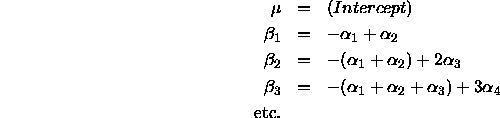
  [to see this, compare model.matrix(coag.sum.aov)[1:4,] with model.matrix(coag.aov)[1:4,] above!]

• contr.poly creates orthogonal polynomials of degree 1, 2, etc., and is most useful for quantitative, rather than qualitative, factors.