To make the procedure as general as possible we rewrite our
demand system in SUR form:![]()
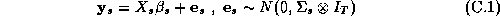
Here the s subscript denotes an individual store, and the dimension of the y vector is M brands by T weeks. In rewriting the model we have stacked the vector of observations for each brand:
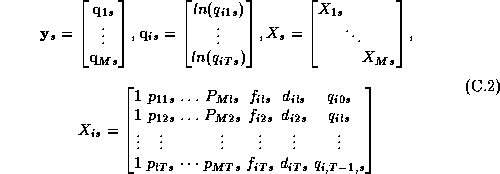
Note that 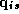 in equation 3.2 refers to the vector of log
movement for a given brand over all weeks, whereas
in equation 3.2 refers to the vector of log
movement for a given brand over all weeks, whereas 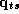 in
equation 2.2 it refers to the vector of log movement across all brands
for a given week. To complete this stage, we also specify natural
conjugate priors using a Wishart distribution on the error covariance
matrix
in
equation 2.2 it refers to the vector of log movement across all brands
for a given week. To complete this stage, we also specify natural
conjugate priors using a Wishart distribution on the error covariance
matrix 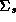 :
:
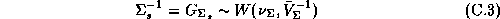
The second stage refers to the hyper-distribution from which the parameters for each store are drawn:
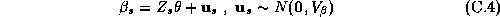
Where all the parameters from a store's demand system (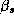 ),
have been stacked into a single vector:
),
have been stacked into a single vector:
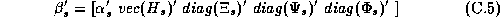
diag(Q) denotes a vector of the diagonal elements from a matrix Q. To
complete this second stage, we include a prior distribution on the
covariance matrix of the second stage 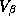 :
:
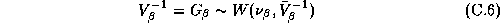
The motivation for
representing 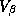 with a prior distribution instead of specifying it
directly is to allow for some uncertainty in the amount of commonalities
across stores.
with a prior distribution instead of specifying it
directly is to allow for some uncertainty in the amount of commonalities
across stores.
The relationships between the demand parameters and the demographic
and competitive variables are contained within the 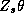 term. We will assume that a consumer's utility function can be
separated along the lines of the price-quality tiers (Blattberg and
Wisniewski 1989). This allows us to place a specific structure upon the
relationship between the demand parameters and demographic variables.
Furthermore each tier will be approximately modified by a linear
function of demographic variables which can be motivated by differences
in household production functions (Becker 1965). We can show that the
cross-price sensitivities within a tier and between tiers have the same
demographic relationships using Lewbel's results (1985). Also, we make
a further modification by allowing the own-price coefficients and
feature coefficients to have their own demographic relationships within
each tier. A formal presentation of these arguments is given in
Montgomery (1994).
term. We will assume that a consumer's utility function can be
separated along the lines of the price-quality tiers (Blattberg and
Wisniewski 1989). This allows us to place a specific structure upon the
relationship between the demand parameters and demographic variables.
Furthermore each tier will be approximately modified by a linear
function of demographic variables which can be motivated by differences
in household production functions (Becker 1965). We can show that the
cross-price sensitivities within a tier and between tiers have the same
demographic relationships using Lewbel's results (1985). Also, we make
a further modification by allowing the own-price coefficients and
feature coefficients to have their own demographic relationships within
each tier. A formal presentation of these arguments is given in
Montgomery (1994).
We can express the linear relationships between the individual coefficients and the demographics as:
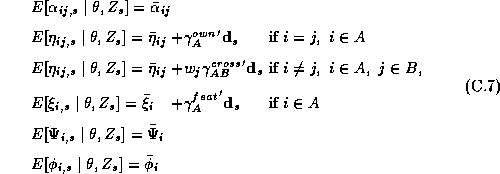
where 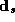 is the vector of demographic and competitive
variables for store s,
is the vector of demographic and competitive
variables for store s, 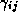 denotes the corresponding
coefficients, and
denotes the corresponding
coefficients, and 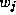 denotes the average market share for product
j
denotes the average market share for product
j![]() . Both of these vectors are
. Both of these vectors are
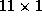 . A and B denotes the set of products within
price-quality tiers A and B, in our application we have three
price-quality tiers. To give the barred constants the
interpretation as chain-wide averages, the
. A and B denotes the set of products within
price-quality tiers A and B, in our application we have three
price-quality tiers. To give the barred constants the
interpretation as chain-wide averages, the 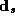 vectors are
standardized with zero means
vectors are
standardized with zero means 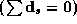 .
.
To illustrate the effects of these common demographic relationships
within the price quality tiers, consider the cross-store variation of
the own-price sensitivities. This 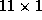 vector will have three
separate demographic effects:
vector will have three
separate demographic effects: 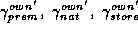 , which correspond with the
premium, national, and store brand tiers respectively. The change in
own-price sensitivity across the stores will have a common demographic
component for all brands within a tier. For example, all three premium
brands will share the same demographic predictor. However, the
individual brands are not restricted to this relationship, since there
will be some random variation about this linear demographic predictor.
Our primary purpose in having these common demographic effects within
each tier is to reduce the number of demographic relationships to a
reasonable number. An alternate specification would have allowed each
parameter to have its own demographic relationship, however this would
have resulted in a highly parameterized model that could present
estimation difficulties. An additional effect of this specification
will be to induce some shrinkage of the changes in the parameter
estimates across stores towards a common tier effect for each store.
This will result in a more limited pattern of shrinkage than Blattberg
and George (1991), which would also shrink parameter estimates within a
store towards one another.
, which correspond with the
premium, national, and store brand tiers respectively. The change in
own-price sensitivity across the stores will have a common demographic
component for all brands within a tier. For example, all three premium
brands will share the same demographic predictor. However, the
individual brands are not restricted to this relationship, since there
will be some random variation about this linear demographic predictor.
Our primary purpose in having these common demographic effects within
each tier is to reduce the number of demographic relationships to a
reasonable number. An alternate specification would have allowed each
parameter to have its own demographic relationship, however this would
have resulted in a highly parameterized model that could present
estimation difficulties. An additional effect of this specification
will be to induce some shrinkage of the changes in the parameter
estimates across stores towards a common tier effect for each store.
This will result in a more limited pattern of shrinkage than Blattberg
and George (1991), which would also shrink parameter estimates within a
store towards one another.
Since all these relationships are linear, we can easily incorporate
them into the 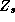 matrix. We can partition
matrix. We can partition 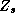 and
and 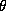 into constants and demographic components:
into constants and demographic components:
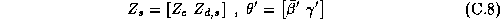
Where the vector of chain-wide averages in the hyper-distribution is:
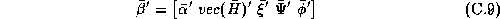
and the relationships with the demographic and competitive variables are given by:

The 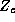 matrix is composed of 1's and 0's and represents the
constant vectors and therefore is the same for each store. In our model
we let each
matrix is composed of 1's and 0's and represents the
constant vectors and therefore is the same for each store. In our model
we let each 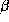 have its own intercept, hence
have its own intercept, hence 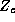 is the
identity matrix with order 192. If certain elements are to be
``shrunk'' toward one another then the corresponding elements in a
particular column are both set to 1, and the other elements set to 0.
is the
identity matrix with order 192. If certain elements are to be
``shrunk'' toward one another then the corresponding elements in a
particular column are both set to 1, and the other elements set to 0.
Since the demographic data vector for each store is the same for
all the parameters, the construction of the 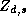 matrix can be
simplified using the following relationship:
matrix can be
simplified using the following relationship:
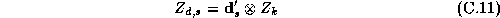
The 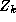 matrix is
constructed in an analogous manner to
matrix is
constructed in an analogous manner to 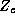 , except that it summarizes
the systematic relationships. In our analysis the
, except that it summarizes
the systematic relationships. In our analysis the 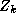 matrix has 15
columns: three columns for the own-price sensitivities (one in each
tier), nine columns for the cross-price sensitivity terms (a full
three by three interaction between the tiers), and three columns for
the feature price coefficients (one in each tier). To illustrate this
matrix consider the column which corresponds to the premium own-price
sensitivities, if the parameter is a premium own-price sensitivity
then the element is set to 1, otherwise the element is 0.
Geometrically this allows for every coefficient to have its own
intercept, but there is a common slope for the own-price elasticities
inside each quality tier.
matrix has 15
columns: three columns for the own-price sensitivities (one in each
tier), nine columns for the cross-price sensitivity terms (a full
three by three interaction between the tiers), and three columns for
the feature price coefficients (one in each tier). To illustrate this
matrix consider the column which corresponds to the premium own-price
sensitivities, if the parameter is a premium own-price sensitivity
then the element is set to 1, otherwise the element is 0.
Geometrically this allows for every coefficient to have its own
intercept, but there is a common slope for the own-price elasticities
inside each quality tier.
The third stage of our model expresses the prior on the hyper-parameters:
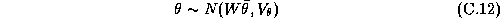
In our specification we will employ a diffuse third
stage prior. But an informative prior on 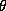 would specify prior beliefs about
chain-wide tendencies or demographic and competitive effects on
parameter variation. The W matrix is included to make the
specification of this prior more flexible.
would specify prior beliefs about
chain-wide tendencies or demographic and competitive effects on
parameter variation. The W matrix is included to make the
specification of this prior more flexible.