So, let me get to the formal stage and that is
how do I put this in this hierarchical Bayesian
model . It's like
putting this grand coefficient framework it fits in really
easily. So I go back and through a judicious choice of stacking
my equations I can go back and have 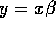 . So y is
going to be my log movement vector, x is going to be all these
covariants, all the prices and demographic effects, I'm sorry,
all the prices and promotional effects. And then I've got this
general error covariance matrix, and then what I'm going to do
in the second stage is say that, look, these
. So y is
going to be my log movement vector, x is going to be all these
covariants, all the prices and demographic effects, I'm sorry,
all the prices and promotional effects. And then I've got this
general error covariance matrix, and then what I'm going to do
in the second stage is say that, look, these 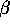 's from up
here, all these price co-efficients, are now going to go to the
second stage of the model. I'm going to say that these store
parameters are related to the demographics and the competitive
characteristics and all the demographic data is in this z
matrix. And then on top of that I've got this relationship, with
these
's from up
here, all these price co-efficients, are now going to go to the
second stage of the model. I'm going to say that these store
parameters are related to the demographics and the competitive
characteristics and all the demographic data is in this z
matrix. And then on top of that I've got this relationship, with
these 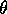 's which is essentially what I've just showed you.
This xxx of characteristics. And then I'm going to take that
down into this third stage.
's which is essentially what I've just showed you.
This xxx of characteristics. And then I'm going to take that
down into this third stage.
Now, also, what's going to be important is how similar are these
individual stores. How big is this random effect? So, in this
case I'm also going to have this 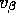 parameters and it's
going to go down here, because I've got to have a prior on where
in the store xxx is. So what the analyst has to provide is this
x, y, z and w. The x is the pricing data, the
y is the
movement data, the z is the demographic data, and then down
here I've got to have another prior on what do I expect the
relationships are going to be. Well, in this case, I'm going to
be confused at this stage of this component on what are these
demographic relationships. Because I don't want to bias the
results, I don't want to say that I know what that education
should have a positive relationship with price elasticity. And
the next step is to go back and say something about, well,
what's my prior on the similarities across the stores. Now that
is going to be important. So, I'm going to have to say something
about you know what is
parameters and it's
going to go down here, because I've got to have a prior on where
in the store xxx is. So what the analyst has to provide is this
x, y, z and w. The x is the pricing data, the
y is the
movement data, the z is the demographic data, and then down
here I've got to have another prior on what do I expect the
relationships are going to be. Well, in this case, I'm going to
be confused at this stage of this component on what are these
demographic relationships. Because I don't want to bias the
results, I don't want to say that I know what that education
should have a positive relationship with price elasticity. And
the next step is to go back and say something about, well,
what's my prior on the similarities across the stores. Now that
is going to be important. So, I'm going to have to say something
about you know what is 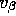 ?
?
For more detail click here.
 Back
Back
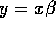 . So y is
going to be my log movement vector, x is going to be all these
covariants, all the prices and demographic effects, I'm sorry,
all the prices and promotional effects. And then I've got this
general error covariance matrix, and then what I'm going to do
in the second stage is say that, look, these
. So y is
going to be my log movement vector, x is going to be all these
covariants, all the prices and demographic effects, I'm sorry,
all the prices and promotional effects. And then I've got this
general error covariance matrix, and then what I'm going to do
in the second stage is say that, look, these 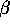 's from up
here, all these price co-efficients, are now going to go to the
second stage of the model. I'm going to say that these store
parameters are related to the demographics and the competitive
characteristics and all the demographic data is in this z
matrix. And then on top of that I've got this relationship, with
these
's from up
here, all these price co-efficients, are now going to go to the
second stage of the model. I'm going to say that these store
parameters are related to the demographics and the competitive
characteristics and all the demographic data is in this z
matrix. And then on top of that I've got this relationship, with
these 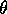 's which is essentially what I've just showed you.
This xxx of characteristics. And then I'm going to take that
down into this third stage.
's which is essentially what I've just showed you.
This xxx of characteristics. And then I'm going to take that
down into this third stage.
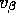 parameters and it's
going to go down here, because I've got to have a prior on where
in the store xxx is. So what the analyst has to provide is this
x, y, z and w. The x is the pricing data, the
y is the
movement data, the z is the demographic data, and then down
here I've got to have another prior on what do I expect the
relationships are going to be. Well, in this case, I'm going to
be confused at this stage of this component on what are these
demographic relationships. Because I don't want to bias the
results, I don't want to say that I know what that education
should have a positive relationship with price elasticity. And
the next step is to go back and say something about, well,
what's my prior on the similarities across the stores. Now that
is going to be important. So, I'm going to have to say something
about you know what is
parameters and it's
going to go down here, because I've got to have a prior on where
in the store xxx is. So what the analyst has to provide is this
x, y, z and w. The x is the pricing data, the
y is the
movement data, the z is the demographic data, and then down
here I've got to have another prior on what do I expect the
relationships are going to be. Well, in this case, I'm going to
be confused at this stage of this component on what are these
demographic relationships. Because I don't want to bias the
results, I don't want to say that I know what that education
should have a positive relationship with price elasticity. And
the next step is to go back and say something about, well,
what's my prior on the similarities across the stores. Now that
is going to be important. So, I'm going to have to say something
about you know what is 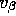 ?
?
 Back
Back