To return to what I was saying. I want to
think about whether I should include the demographics, or how
should I do it. Before I do that, let's think about
some of the possibilities, or how would a non-Bayesian model
this.
Some Possible Approaches
- Individual Store Models
- Large standard errors.
- 192 Parameters for each store, 15,936 total.
A typical thing that marketers would do is simply
say, look, these individual store effects are just really
complicated. It's really pressing my ability just to price at
the chain level, so why should I go out and think about what
these differences are?
- Pooled Models
- Stable estimates and fair predictive ability.
- Ignore store differences.
What I want to do is say
forget about these differences, let's just have the same model
for every store. Obviously from a Bayesian perspective,
this isn't going to be a good idea, because I know something
about why these stores are different. I've got this demographic
information -- why can't I use it?
- Clustered Models
- Price sensitivities are continuous.
A marketer might say, well, let's go to some type of cluster
models. I know the city stores are behaving something
similarly, I know how suburban stores are behaving, so let's
just split these models and say that all the city stores are
similar and all the suburban stores - well, again in this case I'm
losing a lot of information. It's not going to be an
efficient way to do this.
- Fixed Effects
- Sensitive to misspecifications.
Another possibility is to say well,
I would say that there's going to be some kind of fixed
relationship between the demographics and price sensitivity.
Well, they're all errors in model
specification and errors in data measurement and which
variables should we include or not include. The point is
that you can't do these fixed effects, and if you do specify
these fixed effects it's going to be sensitive to your
specification.
A Bayesian Approach
- Random coefficient model that relates the parameters to
characteristics of the store's trading area.
- exploit store commonalities
- allow for store heterogeneity
From the Bayesian perspective what's going to be
good is to recongnize that each of these stores does have some unique
characteristics, but all these stores have something in common.
They're all coming from the same chain, they're all in the same
general area, they're all dealing with consumers who are
exposed to the same types of advertisements over time, so it
makes a lot of sense to say that what's going on here is
probably some kind of random coefficient model. And
I'm going to incorporate this demographic
information at this stage of the model, so I've
got all the parameters from this model that I just
gave, I've got these 192 parameters, let's just think
about one element from this cross-price elasticity matrix.
Let's pull out, for instance, cross-pricing or the cross-price elasticity
of Minute Maid orange juice. So in this case, I'm going to
say that this co-efficient is 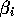 's for an individual store and
it's going to equal some cost-effect across the stores, plus
some kind of demographic effect, plus some type of random
effect. (Click here to see the mathematical form.)
So in this case, 0 this random effect is
really -- I'm going to go back to these individual store
models, or something similar to them. If the demographic effect is strong
and there's not a lot of random error here, it's going to look
something like a fixed effects model. Or if the demographic
effects are nil, and there's not a lot of random error variage
across these parameters, then I'm going to back to this model
case. I'm trying to be inclusive, because I
don't know exactly how strong these relationships are, for all
the reasons I've just stated.
's for an individual store and
it's going to equal some cost-effect across the stores, plus
some kind of demographic effect, plus some type of random
effect. (Click here to see the mathematical form.)
So in this case, 0 this random effect is
really -- I'm going to go back to these individual store
models, or something similar to them. If the demographic effect is strong
and there's not a lot of random error here, it's going to look
something like a fixed effects model. Or if the demographic
effects are nil, and there's not a lot of random error variage
across these parameters, then I'm going to back to this model
case. I'm trying to be inclusive, because I
don't know exactly how strong these relationships are, for all
the reasons I've just stated.
 Previous Section
Previous Section
 Next Section
Next Section
 Go to Table of Contents
Go to Table of Contents
 Go to written version of paper
Go to written version of paper
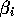 's for an individual store and
it's going to equal some cost-effect across the stores, plus
some kind of demographic effect, plus some type of random
effect. (Click here to see the mathematical form.)
So in this case, 0 this random effect is
really -- I'm going to go back to these individual store
models, or something similar to them. If the demographic effect is strong
and there's not a lot of random error here, it's going to look
something like a fixed effects model. Or if the demographic
effects are nil, and there's not a lot of random error variage
across these parameters, then I'm going to back to this model
case. I'm trying to be inclusive, because I
don't know exactly how strong these relationships are, for all
the reasons I've just stated.
's for an individual store and
it's going to equal some cost-effect across the stores, plus
some kind of demographic effect, plus some type of random
effect. (Click here to see the mathematical form.)
So in this case, 0 this random effect is
really -- I'm going to go back to these individual store
models, or something similar to them. If the demographic effect is strong
and there's not a lot of random error here, it's going to look
something like a fixed effects model. Or if the demographic
effects are nil, and there's not a lot of random error variage
across these parameters, then I'm going to back to this model
case. I'm trying to be inclusive, because I
don't know exactly how strong these relationships are, for all
the reasons I've just stated.
 Previous Section
Previous Section