What ANOVA is

Analysis of variance models (ANOVA models) are used to study the relationship between predictor variables that are not necessarily quantitative and response variables that are quantitative. They are structured like linear regression models, and have the same basic assumptions, but they do not assume a linear relationship between the predictor and response variables.

Example.

Suppose we want to study the relationship between X = the price of a product, and Y = the sales volume in one month.

As a linear regression problem, this is simple. We want to fit the model

But this explicitly assumes that the relationship between price and sales is linear, and this need not be the case, as shown in the figure (for about 70 months' worth of data).

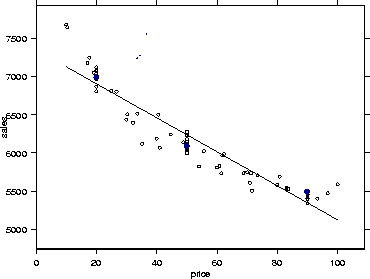
An alternative to fitting the complex nonlinear models we talked about at the end of class last time is to choose a few price points, such as $20.00, $50.00, and $90.00, and define dummy variables

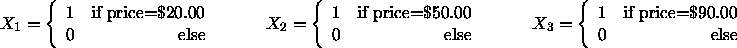
and then fit the regression model

This is an example of a ``one-way ANOVA'' model.

There are three things to note about this approach:

• Even though the model is still the familiar linear regression model, it is possible to detect and explore nonlinearity in the relationship between X and Y, by looking at just these three price levels, or perhaps by adding two or three more price levels to get a better look at the curve. This can be much more efficient than fitting a polynomial or nonlinear regression model.
• It may also be more efficient to collect data for the one-way ANOVA model than for the general regression model; maybe we can get 5 months' worth of data at each of three price points, and have the data collected in a year or so. It is much harder to say how to collect data for this problem if all possible prices are allowed.
• In matrix form this (naive form of the) ANOVA model is

  

  showing that the model is overparameterized (linearly dependent columns).

  All ANOVA models are overparametrized in their ``natural'' form, and we often must make a choice about what a sensible ``reduced'' parametrization is.