Research

Statistical Persistent Homology

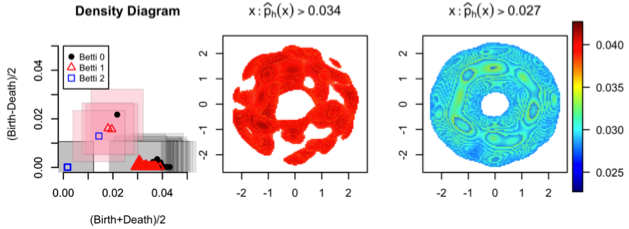
Persistent homology is a method for probing topological properties of point clouds and functions. The method involves tracking the birth and death of topological features as one varies a tuning parameter. Features with short lifetimes are informally considered to be ¡°topological noise.¡± In our work, we attempt bring some statistical ideas to persistent homology. In particular, we have derived confidence intervals that allow us to separate topological signal from topological noise.

Confidence sets for persistence diagrams
Brittany Fasy, Fabrizio Lecci, Alessandro Rinaldo, Larry Wasserman, Sivaraman Balakrishnan, Aarti Singh. [2014]
[ arXiv | Project Euclid | BibTeX ]

Subsampling Methods for Persistent Homology
Frédéric Chazal, Brittany Terese Fasy, Fabrizio Lecci, Bertrand Michel, Alessandro Rinaldo, Larry Wasserman. [2014]
[ arXiv | JMLR | BibTeX ]

On the Bootstrap for Persistence Diagrams and Landscapes
Frédéric Chazal, Brittany Terese Fasy, Fabrizio Lecci, Alessandro Rinaldo, Aarti Singh, Larry Wasserman. [2014]
[ arXiv | Modeling and Analysis of Information Systems | BibTeX ]

Stochastic Convergence of Persistence Landscapes and Silhouettes
Frédéric Chazal, Brittany Terese Fasy, Fabrizio Lecci, Alessandro Rinaldo, Larry Wasserman. [2013]
[ arXiv | BibTeX ]

Minimax Homology Inference

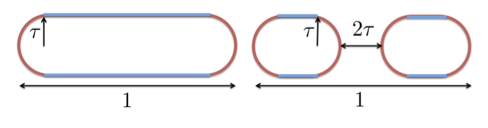
Often, high dimensional data lie close to a low-dimensional submanifold and it is of interest to understand the geometry of these submanifolds. The homology groups of a manifold are important topological invariants that provide an algebraic summary of the manifold. These groups contain rich topological information, for instance, about the connected components, holes, tunnels and sometimes the dimension of the manifold. In this project, we consider the statistical problem of estimating the homology of a manifold from noisy samples under several different noise models. We derive upper and lower bounds on the minimax risk for this problem.

Tight Lower Bounds for Homology Inference
Sivaraman Balakrishnan, Alessandro Rinaldo, Aarti Singh, Larry Wasserman. [2013]
[ arXiv | BibTeX ]

Minimax Rates for Homology Inference
Sivaraman Balakrishnan, Alessandro Rinaldo, Don Sheehy, Aarti Singh, Larry Wasserman. [2011]
[ arXiv | JMLR | BibTeX ]

Filament Estimation

Filaments and Ridges Estimation

A filament is a high density, connected region in a point cloud. There are several methods for estimating filaments but these methods do not provide any measure of uncertainty. We give a definition for the uncertainty of estimated filaments and we study statistical properties of the estimated filaments. We show how to estimate the uncertainty measures and we construct confidence sets based on a bootstrapping technique. We apply our methods to astronomy data and earthquake data.

Asymptotic Theory for Density Ridges
Yen-Chi Chen, Christopher Genovese, Larry Wasserman. [2015]
The Annals of Statistics, Volume 43, Number 5.
[ arXiv | Project Euclid | BibTeX ]

Generalized Mode and Ridge Estimation
Yen-Chi Chen, Christopher Genovese, Larry Wasserman. [2014]
[ arXiv | BibTeX ]

Uncertainty Measures and Limiting Distributions for Filament Estimation
Yen-Chi Chen, Christopher Genovese, Larry Wasserman. [2013]
[ arXiv | BibTeX ]

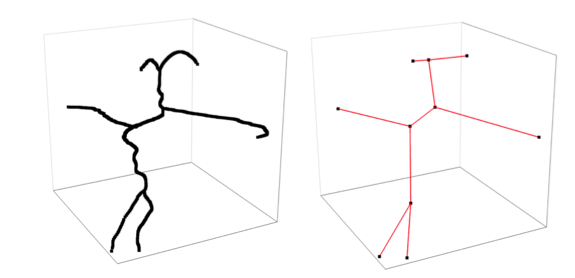
Metric Graph Reconstruction

A metric graph is a 1-dimensional stratified metric space consisting of vertices and edges or loops glued together. Metric graphs can be naturally used to represent and model data that take the form of noisy filamentary structures, such as street maps, neurons, networks of rivers and galaxies. We consider the statistical problem of reconstructing the topology of a metric graph from a random sample. We derive a lower bound on the minimax risk for the noiseless case and an upper bound for the special case of metric graphs embedded in \(\mathbb{R}^{2}\).

Statistical Analysis of Metric Graph Reconstruction
Fabrizio Lecci, Alessandro Rinaldo, Larry Wasserman. [2014]
Journal of Machine Learning Research
[ arXiv | JMLR | BibTeX ]

Cluster Trees

Cluster Trees on Manifolds

In this project we investigate the problem of estimating the cluster tree for a density f supported on or near a smooth d-dimensional manifold M isometrically embedded in R^D. We analyze a modified version of a k-nearest neighbor based algorithm recently proposed by Chaudhuri and Dasgupta. The main results of this paper show that under mild assumptions on f and M, we obtain rates of convergence that depend on d only but not on the ambient dimension D. We also show that similar (albeit non-algorithmic) results can be obtained for kernel density estimators. We sketch a construction of a sample complexity lower bound instance for a natural class of manifold oblivious clustering algorithms. We further briefly consider the known manifold case and show that in this case a spatially adaptive algorithm achieves better rates.

Cluster Trees on Manifolds
Sivaraman Balakrishnan, Srivatsan Narayanan, Alessandro Rinaldo, Aarti Singh, Larry Wasserman. [2013]
Advances in Neural Information Processing Systems 26 (NIPS 2013)
[ arXiv | NIPS | BibTeX ]

DEnsity-BAsed CLustering

Python package DeBaCl The level set tree approach of Hartigan (1975) provides a probabilistically based and highly interpretable encoding of the clustering behavior of a dataset. By representing the hierarchy of data modes as a dendrogram of the level sets of a density estimator, this approach offers many advantages for exploratory analysis and clustering, especially for complex and high-dimensional data. Several R packages exist for level set tree estimation, but their practical usefulness is limited by computational inefficiency, absence of interactive graphical capabilities and, from a theoretical perspective, reliance on asymptotic approximations. To make it easier for practitioners to capture the advantages of level set trees, we have written the Python package DeBaCl for DEnsity-BAsed Clustering.

Mapping Topographic Structure in White Matter Pathways with Level Set Trees
Brian P. Kent, Alessandro Rinaldo, Fang-Cheng Yeh, Timothy Verstynen. [2013]
[ arXiv | BibTeX ]

Manifold Estimation

We consider several problems ranging from the estimation of manifolds in Hausdorff distance, the estimation of filaments in point clouds, and the estimation of ridges of a density function. In each case our study emphasizes the minimax rates.

Nonparametric Ridge Estimation
Christopher R. Genovese, Marco Perone-Pacifico, Isabella Verdinelli, Larry Wasserman. [2014]
The Annals of Statistics, Volume 42, Number 4.
[ arXiv | BibTeX ]

Manifold estimation and singular deconvolution under Hausdorff loss
Christopher R. Genovese, Marco Perone-Pacifico, Isabella Verdinelli, Larry Wasserman. [2012]
The Annals of Statistics, Volume 40, Number 2.
[ arXiv | Project Euclid | BibTeX ]

Minimax Manifold Estimation
Christopher Genovese, Marco Perone-Pacifico, Isabella Verdinelli, Larry Wasserman. [2011]
Journal of Machine Learning Research
[ arXiv | JMLR | BibTeX ]

The Geometry of Nonparametric Filament Estimation
Christopher R. Genovese, Marco Perone-Pacifico, Isabella Verdinelli, Larry Wasserman. [2010]
Journal of the American Statistical Association, Volume 107.
[ arXiv | BibTeX ]

On the path density of a gradient field
Christopher R. Genovese, Marco Perone-Pacifico, Isabella Verdinelli, Larry Wasserman. [2009]
The Annals of Statistics, Volume 40, Number 2.
[ arXiv | Project Euclid | BibTeX ]

AstroStatistics

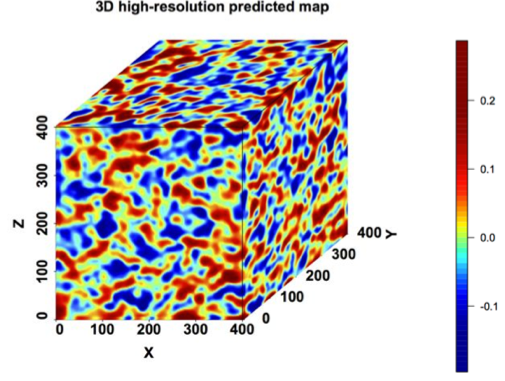
Visualizing the high-redshift Universe is difficult due to the dearth of available data; however, the Lyman-alpha forest provides a means to map the intergalactic medium at redshifts not accessible to large galaxy surveys. Large-scale structure surveys, such as the Baryon Oscillation Spectroscopic Survey (BOSS), have collected quasar (QSO) spectra that enable the reconstruction of HI density fluctuations. The data fall on a collection of lines defined by the lines-of-sight (LOS) of the QSO, and a major issue with producing a 3D reconstruction is determining how to model the regions between the LOS. We present a method that produces a 3D map of this relatively uncharted portion of the Universe by employing local polynomial smoothing, a nonparametric methodology. The performance of the method is analyzed on simulated data that mimics the varying number of LOS expected in real data, and then is applied to a sample region selected from BOSS. Evaluation of the reconstruction is assessed by considering various features of the predicted 3D maps including visual comparison of slices, PDFs, counts of local minima and maxima, and standardized correlation functions. This 3D reconstruction allows for an initial investigation of the topology of this portion of the Universe using persistent homology.

Nonparametric 3D map of the IGM using the Lyman-alpha forest
Jessi Cisewski, Rupert A. C. Croft, Peter E. Freeman, Christopher R. Genovese, Nishikanta Khandai, Melih Ozbek, Larry Wasserman. [2014]
[ arXiv | BibTeX ]

Advanced Data Analysis

Advanced Data Analysis(ADA) is a year long project in Carnegie Mellon University Statistics Ph.D. program. The ADA project is done in collaboration with an investigator from outside the Department, under the guidance of a faculty committee. It culminates in a publishable report that is presented orally and in writing.

Exploring the Intergalactic Medium
Collin Eubanks, Jessi Cisewski, Rupert Croft, Doug Nychka, Larry Wasserman, Kolby Weisenburger
[ Collin’s page ]
The intergalactic medium (IGM) is a diffuse, highly inhomogeneous gas that permeates intergalactic space and hosts a majority of the baryons in the Universe. This matter is too diffuse to be seen by the naked eye; however, its presence is clearly marked by absorption lines in the spectra of luminous, high redshift quasars. We explore nonparametric methods for constructing a 3D map of the neutral hydrogen density fluctuations of the IGM and apply them to the BOSS DR12 data of SDSS-III.

Searching for Voids in MassiveBlack II using Persistent Homology
Jisu Kim, Jessi Cisewski, Tiziana DiMatteo, Alessandro Rinaldo, Larry Wasserman
This project proposes a new approach using persistent homology to find voids in the universe. The proposed method counts the number of statistically significant voids by considering the multi-scale topological structure of the data. Furthermore, the proposed method provides a finer classification of voids with respect to particular topological characteristics.

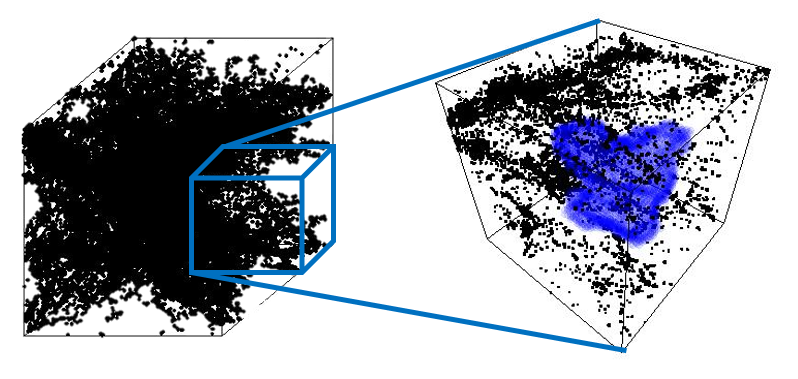
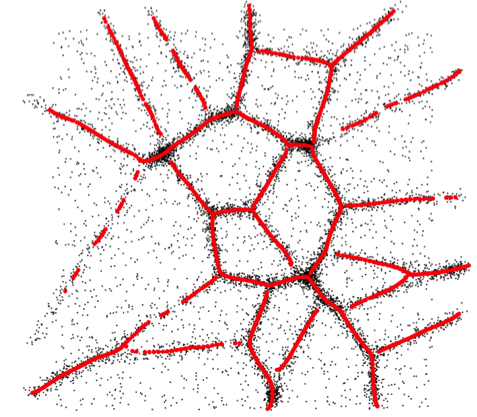
Cosmic Web Reconstruction
Yen-Chi Chen, Shirley Ho, Peter Freeman, Christopher Genovese, Larry Wasserman
[ Yen-Chi’s page | catalogue ]
A filament is a one-dimensional, smooth, connected structure embedded in a multi-dimensional space that characterizes the high density regions. Matter in the Universe tend to aggregate around these filaments which weave our Universe into an intricate network structure. We use ridges of density function (density ridges) as tracers for the filaments and apply our method to the SDSS DR12 to construct a filament catalogue.