This paper takes a general approach to modeling brand competition by constructing a system of demand equations for each store. Each product is modeled as an equation in which its movement is a function of its own price, cross effects of price changes from all other products in the category, and its feature and deal status for that week. This approach avoids imposing a specific substitution pattern on the category. Although a specific market structure could be used to induce a more parsimonious substitution pattern, such as a macro-logit model, or other constraints on the cross-elasticity matrix (Allenby 1989). We avoid imposing a specific market structure to avert rigid forms on market structure, since we are especially interested in whether the market structure is changing from one store to another.
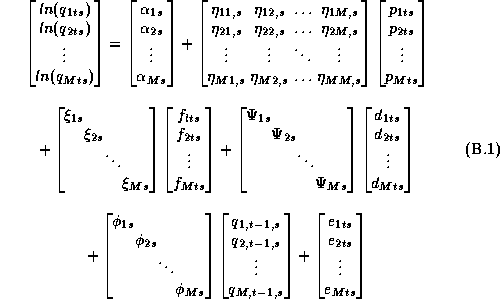
We will model the system of demand equations facing an individual store using a semi-log functional form. This demand system can be expressed as:

Where 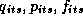 , and
, and 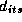 are the log of
movement, price, feature, and deal respectively. The subscript i
denotes the product number, t is week, and s is store. The vector of
error terms,
are the log of
movement, price, feature, and deal respectively. The subscript i
denotes the product number, t is week, and s is store. The vector of
error terms, 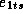 through
through 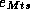 , follows a multivariate normal
distribution with mean 0 and covariance matrix
, follows a multivariate normal
distribution with mean 0 and covariance matrix 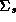 .
The off-diagonal
parameters of the feature, deal, and lag movement variables are zero.
Equation 2.1 can be expressed in matrix form:
.
The off-diagonal
parameters of the feature, deal, and lag movement variables are zero.
Equation 2.1 can be expressed in matrix form:
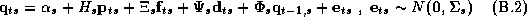
Note that the number of parameters in this system can be very large since a typical category has between 10 and 100 products.
Our position is that these demand models represent a local
approximation to the true demand function. It is a form of particular
interest given its use in the marketing literature. But we do not
declare that this is the only type of approximation that can be used.
A theoretical justification to a similar form of this model is as an
approximation to the multinomial logit demand model implied by the
random utility model which has received a great deal of attention in
the marketing literature (Allenby and Rossi 1991a). While other forms
of approximations have been used, such as in the Rotterdam system
(Clements and Selvanathan 1988, and Vilcassim 1989), we choose this
form for its functional simplicity and stationary time series
properties (i.e., 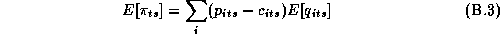 ).
).
The system in 2.1 does not include measures of income, cross-category prices, and competitor prices. In our empirical application it was not possible to obtain accurate measures of these variables. An important assumption in the demand specification for an individual category is that utility for that category is weakly separable from other categories, both in the same store and across stores. Additionally we assume substitution between categories is relatively low. Therefore, as long as the average price changes of the other categories and weekly changes in income are relatively small, we can interpret the coefficients (weighted by their price) as uncompensated price elasticities.