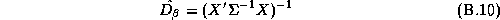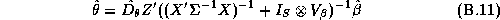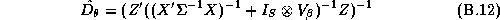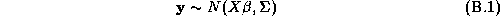
Stacking our individual store models from Chapter 3.2 we have:
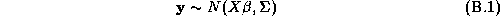
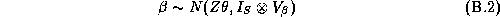
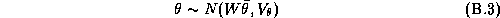
Where the matrices without the store subscript denote the chain-wide information:
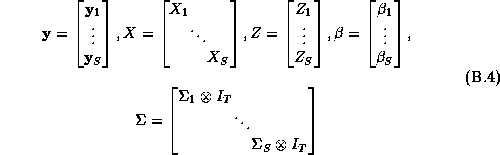
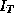 is the identity matrix of dimension T. According to Smith
(1973) if
is the identity matrix of dimension T. According to Smith
(1973) if 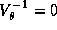 and
and 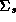 and
and 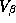 are known
then we can show that the posterior distribution is:
are known
then we can show that the posterior distribution is:
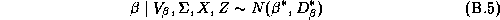
where
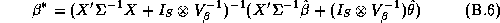
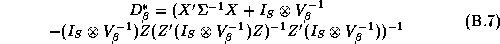
and
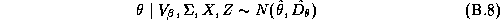
With the LS-estimates defined in the usual way:
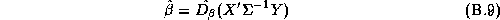
and