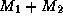 sets of random numbers with each set
being drawn as:
sets of random numbers with each set
being drawn as:
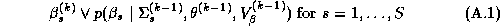
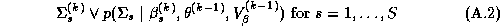
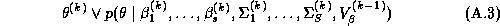
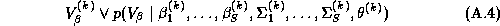
Where 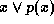 denotes x as a draw from the density
denotes x as a draw from the density
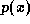 , and k denotes the iteration.
, and k denotes the iteration.
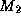 sets of draws to estimate the posterior
marginal distributions.
sets of draws to estimate the posterior
marginal distributions.
The Gibbs sampler requires the solution of the conditional distributions, which can be easily derived due to the hierarchical structure of the model. For a good introduction to the Gibbs sampler see Casella and George (1992). The Gibbs sampler requires sequentially randomly sampling from each of the conditional distributions. It has been shown by Gelfand and Smith (1990) and Gelfand et al. (1990) that these draws converge in distribution to the posterior marginal distributions. The procedure is:
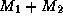 sets of random numbers with each set
being drawn as:
sets of random numbers with each set
being drawn as:
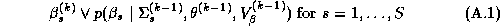
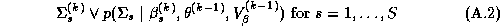
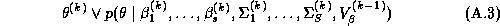
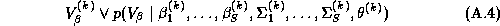
Where 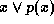 denotes x as a draw from the density
denotes x as a draw from the density
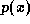 , and k denotes the iteration.
, and k denotes the iteration.
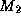 sets of draws to estimate the posterior
marginal distributions.
sets of draws to estimate the posterior
marginal distributions.
This means that the problem reduces to solving the conditional distributions of each parameter. These solutions are readily available due to the model's hierarchical structure and the affine nature of the normal and Wishart distributions (Anderson 1984, pp. 84 and 268-269). The solutions to the conditional distributions are:
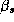 is a SUR model
is a SUR model
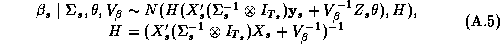
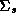 is drawn from an inverted wishart distribution
is drawn from an inverted wishart distribution
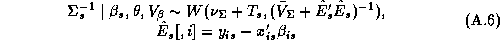
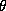 is a multivariate regression
is a multivariate regression
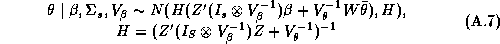
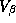 is drawn from an inverted wishart distribution
is drawn from an inverted wishart distribution
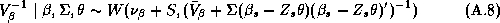
These
conditional distributions are understood to also depend upon the prior
parameters and the data, and Z is a block diagonal matrix with
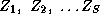 on the diagonal.
The following parameters and data are
supplied by the analyst:
on the diagonal.
The following parameters and data are
supplied by the analyst:
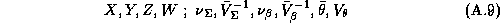
As an additional step in our procedure we also compute the conditional distribution of expected profits. Using the properties of the log-normal distribution we find:
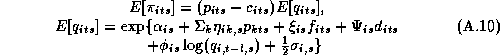
For each store we will sum over all 52 weeks and iterations and divide by the number of iterations, this yields an estimate the marginal posterior profit distribution. Since these calculations are highly computer intensive when applying numerical optimization techniques we use every tenth Gibbs iteration, for a total of 110 iterations. This posterior is conditional only to the given pricing strategy. Therefore no bias is introduced in the profit function as is usually the case when the distribution of the parameter estimates is not accounted for (Blattberg and George 1992).