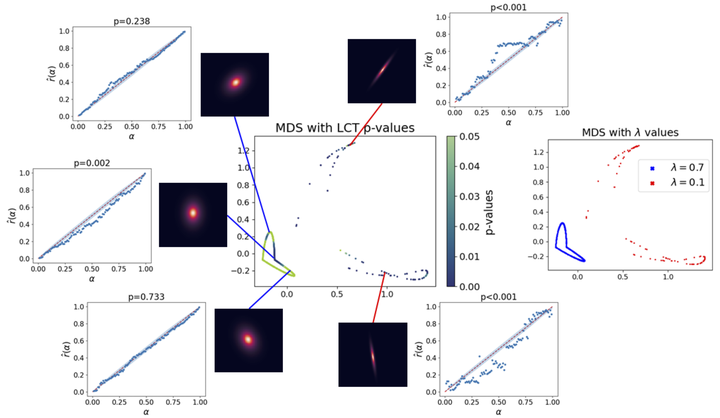
Abstract
There has been growing interest in the AI community for precise uncertainty quantification. Conditional density models f(y|x), where x represents potentially high-dimensional features, are an integral part of uncertainty quantification in prediction and Bayesian inference. However, it is challenging to assess conditional density estimates and gain insight into modes of failure. While existing diagnostic tools can determine whether an approximated conditional density is compatible overall with a data sample, they lack a principled framework for identifying, locating, and interpreting the nature of statistically significant discrepancies over the entire feature space. In this paper, we present rigorous and easy-to-interpret diagnostics such as (i) the ‘Local Coverage Test’ (LCT), which distinguishes an arbitrarily misspecified model from the true conditional density of the sample, and (ii) ‘Amortized Local P-P plots’ (ALP) which can quickly provide interpretable graphical summaries of distributional differences at any location x in the feature space. Our validation procedures scale to high dimensions and can potentially adapt to any type of data at hand. We demonstrate the effectiveness of LCT and ALP through a simulated experiment and applications to prediction and parameter inference for image data.